закрепить навыки и умения доказательства, что данная функция F является первообразной для данной функции f на данном промежутке - ОПРЕДЕЛЕНИЕ ПЕРВООБРАЗНОЙ - ПЕРВООБРАЗНАЯ - 1-е полугодие

Цели: закрепить навыки и умения доказательства, что данная функция F является первообразной для данной функции f на данном промежутке.

Ход урока

I. Устные упражнения

1. Найдите функцию f, если известно, что f'(x) = 3х2.

2. Вместо точек поставьте какую-нибудь функцию, удовлетворяющую равенству:

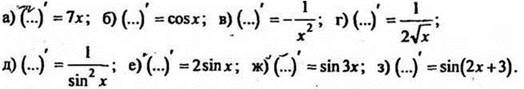
3. Являются ли первообразными для одной и той же функции следующие функции:

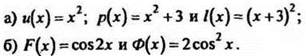
Если являются, то укажите эту функцию.

II. Решение упражнений № 330 (б; г), № 331 (а; б), № 332 (в; б), № 334 (в; г).

III. Самостоятельна работ.

Вариант I

1. Докажите, что функция F есть первообразная для функции f на промежутке (-∞;∞):

2. Найдите одну из первообразных для данной функции на R:

Вариант II

1. Докажите, что функция F есть первообразная для функции f на промежутке (-∞;∞):

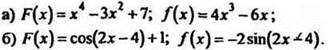
2. Найдите одну из первообразных для данной функции на R:

Вариант III

1. Докажите, что функция F есть первообразная для функции f на промежутке (-∞;0):

2. Является ли функция F первообразной для функции f на промежутке (-∞;∞):

Вариант IV (для сильных учащихся)

1. Является ли функция F первообразной для функций f на промежутке l:

2. Докажите, что функция F есть первообразная для функции f на промежутке l:

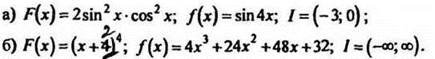
Если сильные учащиеся при решении упражнений из учебника решали быстрее, чем класс, можно самостоятельную работу им выдать раньше.

IV. Итоги урока

V. Домашнее задание: п. 26; № 332 (г), № 333, №334 (а; б); повторить теорему Лагранжа, стр. 128, п. 19.

По желанию:

1. Докажите, что функция F(x) = x3lxl является первообразной для функции f(х) = 4х2|х| на промежутке (-∞;∞).

2. Является ли функция F первообразной для функции f на промежутке l:

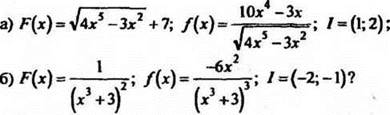
Ответы:

1. При х ≠ 0 равенство F'(x) = f(x) проверяется просто. При х = 0 получаем

2. а) да; б) нет.