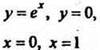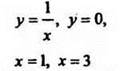закрепить навыки нахождения производных и первообразных логарифмической функции при решении более сложных упражнений - ПРОИЗВОДНАЯ ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ - ПРОИЗВОДНАЯ ПОКАЗАТЕЛЬНОЙ И ЛОГАРИФМИЧЕСКОЙ ФУНКЦИЙ - 2-е полугодие

Цели: закрепить навыки нахождения производных и первообразных логарифмической функции при решении более сложных упражнений.

Ход урока

I. Организационный момент

Устно:

1. Решите уравнение:

2. Найдите первообразную функции на указанном промежутке:

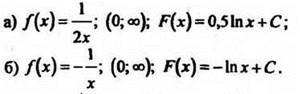
II. Решение упражнений

№ 556 (б; г).

Решение

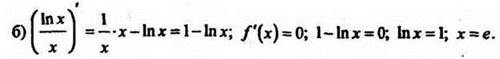
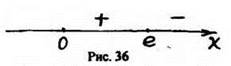
f(x) возрастает при х(0; е], а убывает при [е;∞);

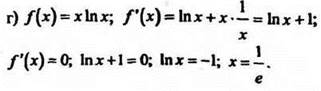
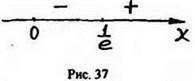
f(x) возрастает при [1/e;∞), а убывает при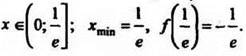

№ 555 (в; а).

Решение

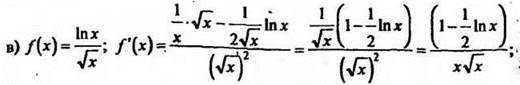
f'(x) = 0 при x = e2.

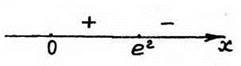
Рис. 38

f(x) возрастает на (0;e2], а убывает на [е2;∞);

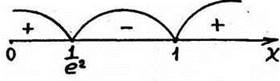
Рис. 39

f(х) возрастает при х(0;1/e2], [1;∞) и убывает при х[1/e2;1]; имеет максимум в точке 1/e2 и минимум в точке 1;

№ 557 (b).

Решение

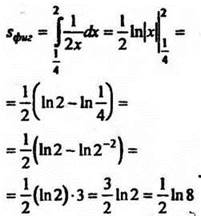
III. Самостоятельная работа

Задание		Ответ
Вариант I	Вариант II	1	2	3	4
Найдите f'(0), если		-2	-1	1	2
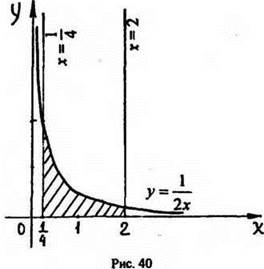
Вычислите площадь фигуры, ограниченной линиями:		1,1	2,8	1,2	1,7
Найдите промежутки возрастания функции		[1; ∞)	(∞; 1]	(-∞; 2]	[2; ∞)

Верный ответ: вариант I - 3, 4, 2; вариант II - 4, 1, 3.

IV. Итоги урока

V. Домашнее задание: § 11, п. 41, 42; № 556 (б; г), № 557 (а; б; г).