продолжить решение задач по изученной теме, проверить навык их решения - ПОНЯТИЕ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ - ПРОИЗВОДНАЯ ПОКАЗАТЕЛЬНОЙ И ЛОГАРИФМИЧЕСКОЙ ФУНКЦИЙ - 2-е полугодие

Цели: продолжить решение задач по изученной теме, проверить навык их решения.

Ход урока

I. Проверка домашнего задания

Вынести решение № 578 на доску. Ответить на вопросы учащихся.

Собрать задачи на применение дифференциальных уравнений.

II. Решение упражнений

№ 579.

Решение

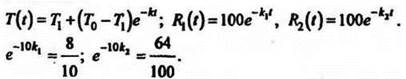
Требуется найти момент времени t, когда R1(t) – R2(t) = 25, т. е.

Обозначим t/10 = х, получи.

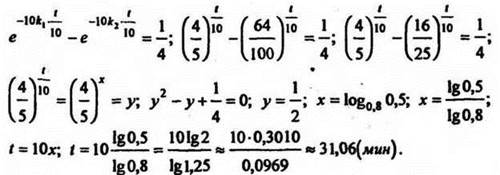
№ 580.

Решение

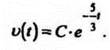Для определения постоянной С подставим t = 0:

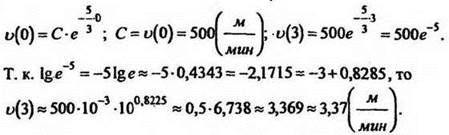
III. Самостоятельная работ.

Вариант I

1. Докажите, что функция удовлетворяет дифференциальному уравнению

2. Найдите такое решение дифференциального уравнения что f(0) = 5.

3. Запишите дифференциальное уравнение гармонического колебания

Вариант II

1. Докажите, что функция удовлетворяет дифференциальному уравнению

2. Запишите общий вид решения дифференциального уравнения Найдите решение этого уравнения, удовлетворяющее условию y(0) = е.

Вариант III

1. Докажите, что функция удовлетворяет дифференциальному уравнению у’ = -2у.

2. Запишите общий вид решения дифференциального уравнения Найдите решение этого уравнения, удовлетворяющее условию у(1) = е.

Вариант IV

1. Запишите дифференциальное уравнение, которому удовлетворяет функция

2. Найдите решение дифференциального уравнения такое, что f(1) = 2.

3. Запишите общий вид решений дифференциального уравнения

Во время самостоятельной работы отобрать наиболее удачные задачи, принесённые учащимися для домашнего задания. Часть поместить на стенд в классе.

IV. Итоги урока

V. Домашнее задание: § 11, п. 41-44. Подготовиться к контрольной работе.

Домашняя контрольная работа

Вариант 1

1. а) Дана функция Найдите f'(х); f'(0);

б) дана функция Найдите '(х); ’(-1/8).

2. Вычислите площадь фигуры, ограниченной линиями у = ех ; у = 1; х = 2.

3. Исследуйте на возрастание (убывание) и на экстремумы функцию

4. Докажите, что функция удовлетворяет дифференциальному уравнению у’ = -2у.

Вариант II

1. а) Дана функция Найдите f'(x); f'(0):

б) дана функция 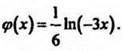Найдите '(х); ’(-1/9).

2. Вычислите площадь фигуры, ограниченной линиями у = 1/x; у = 1; х = 4.

3. Исследуйте на возрастание (убывание) и на экстремумы функцию

4. Удовлетворяет ли функция дифференциальному уравнению

Вариант III

1. а) Дана функция Найдите f'(х); f'(0).

б) дана функция Найдите '(х); ’(1/2).

2. Вычислите площадь фигуры, ограниченной линиями у = е-x; у = 1; х = -2.

3. Исследуйте иа возрастание (убывание) и на экстремумы функцию

4. Удовлетворяет ли функция дифференциальному уравнению f’(x) = 3f(x)?

Вариант IV

1. а) Дана функция Найдите f'(x); f'(0);

б) дана функция Найдите '(х); ’(1/3).

2. Вычислите площадь фигуры, ограниченной линиями у = 2/x; у = 2; х = 3.

3. Исследуйте на возрастание (убывание) и на экстремумы функцию

4. Период полураспада радиоактивного вещества равен 3 ч. Через какой промежуток времени от 8 кг этого радиоактивного вещества останется 0,25 кг?