Подготовка к зачету по теме «Рациональные дроби» - ПРОИЗВЕДЕНИЕ И ЧАСТНОЕ ДРОБЕЙ - РАЦИОНАЛЬНЫЕ ДРОБИ

Цель: решение задач по теме «Рациональные дроби и их свойства».

Ход урока

I. Сообщение темы и цели урока

II. Основные понятия

При необходимости напомните основные сведения по данной теме (уроки 1 — 23).

Целые выражения — выражения, составленные из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, не равное нулю:

Дробные выражения — выражения, содержащие деление на выражение с переменными:

Рациональные выражения включают в себя целые и дробные выражения. Допустимые значения переменных — значения переменных, при которых выражение имеет смысл. В рациональных выражениях допустимыми являются те значения переменных, при которых не равен нулю знаменатель.

Выполняется основное свойство дроби: (при b ≠ 0 и с ≠ 0), т. е. числитель и знаменатель дроби можно умножить на число, не равное нулю.

Свойства дробей

1. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тем же, т. е. При сложении дробей с разными знаменателями дроби приводят к общему знаменателю.

2. Чтобы умножить дроби, нужно умножить их числители и умножить их знаменатели. Первое произведение записать числителем, а второе произведение — знаменателем дроби, т. е.

3. Чтобы возвести дробь в степень, нужно возвести в эту степень числитель и знаменатель. Первый результат записать в числителе, второй результат — в знаменателе дроби, т. е.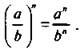

4. Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй, т. е.

Сумму, разность, произведение и частное рациональных дробей всегда можно представить в виде рациональной дроби. Поэтому всякое рациональное выражение можно представить в виде рациональной дроби.

Обратная пропорциональность — функция, которую можно задать формулой вида y = k/x, где х — независимая переменная и k — число, не равное нулю.

III. Задание на уроке

№ 188 (а, г); 194 (в, д); 200 (а, г); 210 (г); 219 (а); 230 (а); 242 (а, б); 250 (а).

IV. Задание на дом

№ 188 (в, е); 194 (б, г); 201 (а, в); 211 (в); 220 (г); 232, 242 (в, г); 250 (б).

V. Подведение итогов урока