Уравнение х2 = a - ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА - КВАДРАТНЫЕ КОРНИ

Цель: рассмотреть решение простейшего квадратного уравнения.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Вычислите:

2. Решите уравнение и неравенство:

Вариант 2

1. Вычислите:

2. Решите уравнение и неравенство:

III. Изучениие нового материала (основные понятия)

Рассмотрим простейшее квадратное уравнение х2 = а (где а — произвольное число). В зависимости от числа а при решении этого уравнения возможен один из трех случаев.

1. Если а < 0, то данное уравнение корней не имеет. Действительно, для любого числа х левая часть уравнения х2 ≥ 0, а правая часть — число а < 0. Получаем противоречие: неотрицательная величина не может равняться отрицательному числу.

2. Если а = 0, то уравнение имеет единственный корень, равный нулю (т. е. корень x = 0). Только для числа х = 0 величина х2 = 0 и уравнение обращается в верное равенство.

3. Если а > 0, то уравнение имеет два корня Действительно, при подстановке в данное уравнение числа получаем: (верное равенство), при подстановке значения имеем: (также верное равенство).

Три возможных случая решения уравнения х2 = а имеют простую графическую иллюстрацию. Построим график функции у1 = х2 (парабола). Для различных значений а построим график функции у2 = а (прямая, параллельная оси абсцисс).

В случае а < 0 прямая у2 (прямая 1) расположена ниже оси абсцисс и не имеете параболой у общих точек. Поэтому данное уравнение решений не имеет.

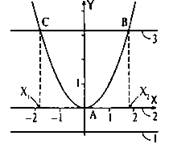
В случае а = 0 прямая у2 (прямая 2) совпадает с осью абсцисс и имеет с параболой y1 одну общую точку A, абсцисса которой х = 0. Поэтому данное уравнение имеет единственный корень х = 0.

В случае а > 0 прямая у2 (прямая 3) расположена выше оси абсцисс и пересекает параболу у1 в двух точках В и С. Так как парабола y1 симметрична относительно оси ординат, то точки В и С также симметричны относительно оси ординат. Пусть абсциссы этих точек х2 и х1 соответственно. Так как х2 есть положительное число, квадрат которого равен а, то х2 является арифметическим квадратным корнем из a, т. е. х2 = Так как х1 есть число, противоположное х2, то

Пример 1

а) Уравнение х2 = 16 имеет два корня

б) Уравнение х2 = 3 также имеет два корня Эти корни являются иррациональными числами, т. к. не существует рационального числа, квадрат которого равен 3 (доказательство было приведено в уроке 28).

Пример 2

Решим уравнение (х - 2)2 = 6,25.

Обозначим буквой Z величину х - 2 (т. е. Z = x - 2) и получим простейшее квадратное уравнение Z2 = 6,25. Это уравнение имеет два корня: Теперь вернемся к старой неизвестной х и получим два линейных уравнения: х - 2 = -2,5 (его корень х1 = -0,5) и х - 2 = 2,5 (его корень х2 = 4,5). Итак, данное уравнение имеет два корня х1 = -0,5 и х2 = 4,5.

Пример 3

Решим уравнение х2 - 6х + 5 = 0.

Ранее такие квадратные уравнения мы решали разложением левой части на множители. Используем теперь для решения другой способ — выделение полного квадрата разности. Рассмотрим первые два слагаемые х2 - 6х в левой части уравнения и запишем их в виде х2 - 2 · х · 3, т. е. квадрат первого числа минус удвоенное произведение первого числа на второе (в качестве второго числа возьмем число 3). Если добавить (соответственно и вычесть) квадрат второго числа 32 = 9, то получим полный квадрат разности: (х2 - 6х + 9) - 9 + 5 = 0, или (х - 3)2 - 4 = 0, или (х - 3)2 = 4. Далее уравнение решается аналогично предыдущему примеру. Получаем два линейных уравнения: х - 3 = -2 (его корень х1 = 1) и х - 3 = 2 (корень х2 = 5). Итак, уравнение имеет два корня х1 = 1 и х2 = 5.

Пример 4

Определим число корней уравнения х2 + 4х + с = 0 (где с — произвольное число).

Для анализа этого уравнения также используем способ выделения полного квадрата суммы. Для этого в левой части уравнения добавим (и вычтем) число 4. Получаем: (х2 + 4х + 4) + с - 4 = 0 или (х + 2)2 = 4 – с. С помощью обозначений Z = x + 2 и a = 4 - с это уравнение сводится к простейшему квадратному уравнению Z2 = а.

При а < 0 или 4 - с < 0 (т. е. с > 4) это (и данное) уравнение корней не имеет.

При а = 0 или 4 - с = 0 (т. е. с = 4) уравнение имеет один корень.

При а > 0 или 4 - с = 0 (т. е. с < 4) уравнение Z2 = а имеет два корня Z1 и Z2. Вернувшись к старой неизвестной Z = х + 2, получаем, что и данное уравнение имеет два корня х1 и х2.

Заметим, что в задачах с параметрами ответ принято записывать в порядке возрастания параметра. Поэтому в рассмотренном примере ответ имеет вид: при с < 4 — два корня, при с = 4 — один корень, при с > 4 — нет корней.

IV. Контрольные вопросы

1. Возможные случаи решения уравнения х2 = а.

2. Графическое решение уравнения х2 = а (три случая).

V. Задание на уроке

№ 306 (а, б); 307 (в); 309 (а, д); 310 (а, б); 311 (а, в); 312; 315; 317 (а, в).

VI. Задание на дом

№ 305 (а, в, г); 307 (г); 308 (б); 309 (б, з); 311 (б, г); 314; 316 (а, д, е, з); 317 (б, г); 318 (г).

VII. Творческие задания

1. Решить уравнение:

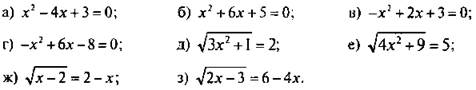
Ответы: а) х1 = 1 и х2 = 3; б) х1 = -1 и х2 = -5; в) х1 = -1 и х2 = 3; г) х1 = 2 и х2 = 4; д) х1 = -1 и х2 = 1; е) х1 = -2 и х2 = 2; ж) х = 2; з) х = 1,5.

2. Определите число корней уравнения:

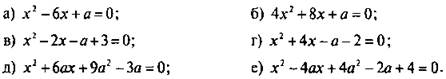
Ответы: а) при а < 9 - 2 корня, при а = 9 - 1 корень, при а > 9 — нет корней;

б) при а < 4 — 2 корня, при а = 4 - 1 корень, при а > 4 — нет корней;

в) при а < 2 — нет корней, при а = 2 - 1 корень, при а > 2 - 2 корня;

г) при а < -6 — нет корней, при a = -6 - 1 корень, при а > -6 - 2 корня;

д) при а < 0 - нет корней, при а = 0 - 1 корень, при а > 0 - 2 корня;

е) при а < 2 — нет корней, при а = 2 - 1 корень, при а > 2 - 2 корня.

VIII. Подведение итогов урока