Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева

Сравнение чисел. Числовые неравенства - ЧИСЛОВЫЕ НЕРАВЕНСТВА И ИХ СВОЙСТВА - НЕРАВЕНСТВА

Цель: рассмотреть сравнение чисел и значений алгебраических выражений.

Ход урока

I. Сообщение темы и цели урока

II. Изучение нового материала (основные понятия)

Можно сравнить два любых числа a и b результат сравнения записать в виде равенства или неравенства, используя знаки =, <, >. Очевидно, что для чисел а и b выполняется только одно из соотношений: а = b или а > b, или а < b. Рассмотрим примеры сравнения чисел.

Пример 1

Сравним положительные обыкновенные дроби 5/9 и 6/77. Для этого приведем данные к общему знаменателю 99 и получим: и Знаменатели дробей 55/99 и 54/99 одинаковы, но числитель первой дроби 55 больше, чем числитель 54 второй дроби (т. е. 55 > 54). Поэтому первая дробь больше второй или

Пример 2

Сравним положительные десятичные дроби 2,716 и 2,72. Цифры в разрядах единиц и десятых у двух данных дробей одинаковы. В разряде сотых первой дроби стоит цифра 1, а второй дроби — цифра 2. Так как 1 < 2, то первая дробь меньше, чем вторая, т. е. 2,716 < 2,72.

Пример 3

Сравним положительные обыкновенную дробь 7/20 и десятичную дробь 0,35. Для этого обратим обыкновенную дробь 7/20 в десятичную и получим 7/20 = 0,35 (т. е. данные числа равны). Заметим, что можно сделать и наоборот — обратить десятичную дробь в обыкновенную. Тогда получим: (т. е. данные числа равны).

Пример 4

Сравним отрицательные числа -17 и -22. Найдем модули данных чисел: |-17| = 17 и |-22| = 22. Так как модуль первого отрицательного числа меньше модуля второго отрицательного числа (т. е. 17 < 22), то само первое число больше второго, т. е. -17 > -22.

Заметим, что в примерах 1—4 в зависимости от конкретного вида чисел использовался тот или иной способ сравнения. Очевидно, что удобно использовать универсальный способ сравнения чисел, охватывающий все случаи. В таком способе находится разность данных чисел и сравнивается с нулем (т. е. определяется, является ли эта разность положительным числом, отрицательным числом или нулем). Этот способ сравнения основан на следующем определении.

Число а больше числа b, если разность a - b — положительное число; число а меньше числа b, если разность a - b — отрицательное число; числа а и b равны, если разность a - b равна нулю. Для удобства такое определение приведено в таблице.

Разность чисел	a - b > 0	а – b < 0	а – b = 0
Соотношение между числами	a > b	а < b	а = b

На координатной прямой большее число изображается точкой, лежащей правее, а меньшее — точкой, лежащее левее. Рассмотрим некоторые числа а и b. Обозначим их разность а - b буквой с. Так как а - b = с, то а = b + с. Если с — положительное число, то точка с координатой b + с лежит правее точки с координатой b или точка а лежит правее точки с координатой b, т. е. а > b.

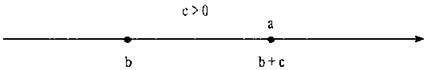
Если с — отрицательное число, то точка с координатой b + с лежит левее точки с координатой b или точка а лежит левее точки с координатой b, т. е. а < b.

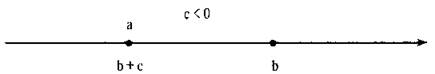
Если с равно нулю, то точка с координатой b + с совпадает с точкой с координатой h или точки а и b совпадают, т. е. а = b.

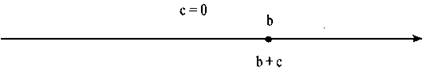
Приведенное определение очень часто используется при сравнении чисел: все примеры 1-4 могут быть сделаны с помощью универсального способа.

Пример 5

Еще раз вернемся к примеру 1 и сравним дроби 5/9 и 6/11. Найдем разность этих дробей Так как эта разность положительна (т. е. ), то первое число больше второго, т. е. (по определению).

Универсальный способ удобен и при сравнении значений алгебраических выражений.

Пример 6

При любых значениях переменной а сравним значения выражений (a – 2)(a - 7) и (а – 4)(a - 5).

Найдем разность данных выражений:

При любом значении а рассматриваемая разность отрицательна. Поэтому по определению первое выражение меньше второго, т. е.

Пример 7

Если числа a ≥ 0 и b ≥ 0, то выполняется неравенство

Заметим, что выражение называется средним арифметическим чисел а и b, выражение называется средним геометрическим чисел а и b. Поэтому неравенство называется неравенством между средним арифметическим и средним геометрическим. Докажем это неравенство двумя способами: алгебраическим и геометрическим.

Алгебраический способ. Рассмотрим разность чисел и определим знак этой разности, выделив полный квадрат разности. Получаем: Числитель этой дроби при всех значениях а ≥ 0 и b ≥ 0 неотрицателен, знаменатель положителен. Поэтому величина Тогда по определению получаем Дробь при т. е. при или а = b.

Итак, неравенство между средним арифметическим и средним геометрическим выполняется и превращается в равенство только при a = b.

Геометрический способ. На прямой l построим отрезки АВ (длиной а) и ВС (длиной b).

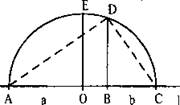
Найдем середину отрезка АС — точку О. Из этой точки радиусом проведем полуокружность. К прямой l из точек О и В восстановим перпендикуляры ОЕ и BD до их пересечения с полуокружностью. Тогда длина отрезка — среднее арифметическое чисел а и b. Докажем, что длина отрезка — среднее геометрическое чисел a и b. Для этого рассмотрим прямоугольные треугольники ABD и CBD. Они подобны, т. к. ∠ABD = ∠CBD = 90° и ∠BAD = ∠BDC (углы со взаимно перпендикулярными сторонами). Учтем пропорциональность сторон: откуда BD2 = ab и .