Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Построение графика функции y = ax2 + bх + с - ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ - КВАДРАТИЧНАЯ ФУНКЦИЯ
Цель: рассмотреть методику построения графика квадратичной функции.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Как определить координаты вершины параболы y = ax2 + bх + с?
2. Для квадратичной функции у = -х2 + 4х – 3:
а) постройте график (параболу);
б) найдите точки пересечения с осями координат;
в) найдите координаты вершины параболы;
г) найдите промежутки возрастания и убывания функции, ее наибольшее значение.
Вариант 2
1. Как определить направление ветвей параболы и ось симметрии параболы у = ах2 + bх + с?
2. Для квадратичной функции у = -х2 + 2х + 3:
а) постройте график (параболу);
б) найдите точки пересечения с осями координат;
в) найдите координаты вершины параболы;
г) найдите промежутки возрастания и убывания функции, ее наибольшее значение.
III. Изучение нового материала (основные понятия)
На примере рассмотрим алгоритм построения графика квадратичной функции.
Пример 1
Построим график функции у = х2 - 2х - 3.
1. Найдем координаты вершины параболы: ![]() у0 = y(х0) = 12 - 2 - 3 = -4. Построим вершину — точку (1; -4).
у0 = y(х0) = 12 - 2 - 3 = -4. Построим вершину — точку (1; -4).
2. Проведем через эту точку А(1; -4) прямую x = 1, параллельную оси ординат, — ось симметрии параболы (рис. а).
3. Найдем точки пересечения параболы с осью абсцисс. Для этого решим уравнение 0 = у(х) или 0 = x2 – 2x – 3. Получаем корни этого квадратного уравнения х1 = -1 и х2 = 3. Построим эти точки пересечения с осью абсцисс В(-1; 0) и С(3; 0) (рис. б).
4. Найдем точку пересечения параболы с осью ординат. Для этого в уравнении параболы положим х = 0 и найдем y(0) = 02 - 2 · 0 - 3 = -3. Построим точку D(0; -3) (рис. б).
5. Через характерные точки А, В, С и D квадратичной функции проведем параболу (рис. в).
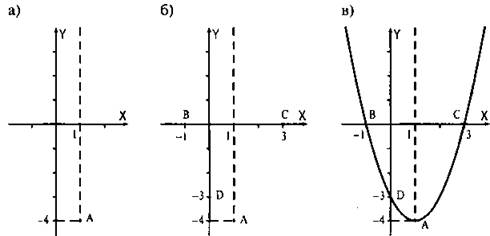
Заметим, что всегда рисуется только эскиз графика. Поэтому для построения эскиза параболы перечисленных четырех точек достаточно. Для более точного построения параболы можно взять еще несколько пар точек, симметричных относительно оси симметрии параболы.
Аналогично рассмотренному примеру можно построить график любой квадратичной функции y = ax2 + bx + c.
1. Найдем координаты вершины параболы (х0; у0) по формулам х0 = -b/2a и у0 = y(x0). Построим вершину параболы (x0; y0).
2. Проведем через вершину параболы (х0; у0) прямую x = х0, параллельную оси ординат, - ось симметрии параболы.
3. Найдем точки пересечения параболы с осью абсцисс. Для этого определим нули функции y(x), решив квадратное уравнение у(х) = 0. Отметим эти точки на оси абсцисс.
4. Найдем точку пересечения параболы с осью ординат. Для этого в уравнении параболы положим х = 0 и найдем y(0). Отметим эту точку на оси ординат.
5. Проведем через построенные точки параболу.
6. Заметим, что для более точного построения графика полезно найти еще несколько точек параболы. Для этого надо взять две точки на оси Ох, симметричные относительно точки х0, и вычислить соответствующие значения функции (такие значения равны). Например, можно взять пары точек: 1/2x0 и 3/2x0; 0 и x0; -1/2x0 и 5/2х0 и т. д. (если х0 ≠ 0).
Пример 2
Построим график функции у = -х2 - 2х + 3 и обсудим свойства этой функции.
1. Найдем координаты вершины параболы: ![]() и
и ![]() Построим ось симметрии параболы — прямую x = -1.
Построим ось симметрии параболы — прямую x = -1.
2. Найдем точки пересечения параболы с осью абсцисс, решив квадратное уравнение у(x) = 0 или -х2 - 2х + 3 = 0. Его корни x1 = -3 и х2 = 1. Отметим эти точки на оси абсцисс.
3. Найдем точку пересечения параболы с осью ординат. В уравнении параболы положим х = 0 и найдем у(0) = 3. Отметим эту точку на оси ординат.
4. Через отмеченные точки проведем параболу. График функции построен.
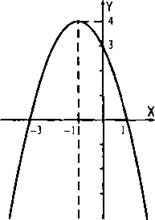
Обсудим теперь свойства этой квадратичной функции:
1) Значения функции положительны при -3 < х < 1 и отрицательны при х < -3 и х > 1. Значение функции равно нулю при х = -3 и х = 1.
2) Функция возрастает на промежутке х ≤ -1 и убывает на промежутке х ≥ -1. При х = -1 функция принимает наибольшее значение у = 4. При любых значениях х значения функции меньше или равны 4.
3) График функции симметричен относительно прямой х = -1.
Функция y=ax2 + bх + с принимает наименьшее или наибольшее значение в точке х0 = -b/2a, которая является абсциссой вершины параболы. Это значение (значение функции в точке х0) можно найти по формуле у0 = у(х0).
Если а > 0, то функция имеет наименьшее значение; если а < 0, то функция имеет наибольшее значение.
Например, в примере 1 функция у = х2 - 2х -3 при х = 1 принимала наименьшее значение у = -4. В примере 2 функция у = -х2 - 2х + 3 при х = -1 принимала наибольшее значение у = 4.
Пример 3
Сумма двух чисел равна 8. Сумма кубов этих чисел наименьшая. Найти эти числа и сумму их кубов.
Пусть первое из этих чисел х, тогда второе число равно 8 - х. Найдем сумму кубов этих чисел у ![]()
![]() Для параболы y = 24х2 - 192х + 512 коэффициент а = 24 > 0. Поэтому такая функция принимает наименьшее значение. Найдем координаты вершины этой параболы:
Для параболы y = 24х2 - 192х + 512 коэффициент а = 24 > 0. Поэтому такая функция принимает наименьшее значение. Найдем координаты вершины этой параболы: ![]() и
и ![]() Итак, при х0 = 4 функция принимает наименьшее значение, равное 128. Таким образом, если оба данных числа равны 4, то сумма кубов этих чисел равна 128 и является наименьшей.
Итак, при х0 = 4 функция принимает наименьшее значение, равное 128. Таким образом, если оба данных числа равны 4, то сумма кубов этих чисел равна 128 и является наименьшей.
Пример 4
На рисунке приведен график функции у = ах2 + bх + с. Определите знаки коэффициентов a, b и с.
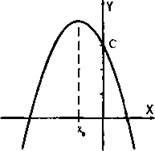
1) Так как ветви параболы направлены вниз, то коэффициент а < 0.
2) Абсцисса х0 вершины параболы отрицательна (как видно из рисунка).
Получаем неравенство –b/2a < 0. Умножим обе его части на отрицательное число 2а. При этом знак неравенства меняется на противоположный. Получаем -b > 0. Вновь умножим обе части этого неравенства на отрицательное число -1. Опять знак неравенства меняется на противоположный. Имеем b < 0. Значит, коэффициент b < 0.
3) При х = 0 значение функции y(х) равно y(0) = с. Из рисунка видно, что с > 0.
Итак, были определены знаки коэффициентов: a < 0, b < 0 и с > 0.
Пример 5
На рисунке приведен график функции у = ах2 + bх + с. Определите знак выражения: а) а + b + с; б) 4а – 2b + с.
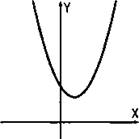
Видно, что при всех значениях х функция у(х) принимает только положительные значения. Осталось понять смысл данных выражений. Найдем значение функции у = ах2 + bх + с
а) при х = 1 у(1) = а + b + с;
б) при х = -2 y(-2) = a · (-2)2 + b · (-2) + c = 4a - 2b + c.
Напомним, что при всех значениях х (в т. ч. и при х = 1, и при х = -2) значения функции положительны. Поэтому a + b + c > 0 и 4а – 2b + с > 0.
Пример 6
График квадратичной функции у = ах 2+ bх + с проходит через точку A(-1; 10) и имеет вершину в точке В(1; -2). Напишите уравнение параболы.
Запишем условия прохождения параболы через точки A и В. Кроме того, учтем, что точка В — вершина параболы. Запишем выражение для абсциссы вершины. Получаем систему уравнений: 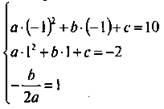 или
или 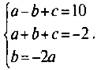
Вычтем из первого уравнения второе и получим -2b = 12, откуда b = -6. Тогда из третьего уравнения имеет -6 = -2а, откуда а = 3. Подставим значения а = 3 и b = -6 в первое уравнение и получим: 3 + 6 + с = 10, откуда с = 1.
Таким образом, напишем уравнение данной параболы у = 3х2 - 6х + 1.
Пример 7
Найти значение параметра к, при котором прямая у = 2х - 5 касается параболы у = х2 + kх + 4. Найти координаты точки касания.
Если графики двух функций пересекаются в точке с координатами (х0; у0),то величины x0, и у0 являются решением системы уравнений 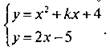 Если (х0; у0) — точка касания двух графиков, то приведенная система имеет единственное решение (х0; y0).
Если (х0; у0) — точка касания двух графиков, то приведенная система имеет единственное решение (х0; y0).
Приравняем правые части уравнений системы: х2 + kх + 4 = 2х - 5 и получим х2 + (k - 2)х + 9 = 0. Это уравнение (а следовательно, и приведенная система) имеет единственное решение, если дискриминант D = (k – 2)2 – 4 · 9 = k2 – 4k - 32 = 0. Корни этого уравнения k1 = -4 и k2 = 8.
а) При k = -4 уравнение х2 + (k - 2)х + 9 = 0 имеет вид х2 - 6х + 9 = 0 или (х - 3)2 = 0. Корень этого уравнения х = 3, тогда у = 2х - 5 = 2 · 3 - 5 = 1. Итак, при k = -4 данные парабола и прямая касаются в точке (3; 1).
б) При k = 8 уравнение x2 + (k - 2)х + 9 = 0 имеет вид х2 + 6х + 9 = 0 или (х + 3)2 = 0. Корень этого уравнения х = -3, тогда y = 2х - 5 = 2 · (-3) - 5 = -11. Итак, при k = 8 данные парабола и прямая касаются в точке (-3; -11).
IV. Контрольные вопросы
При построении графика квадратичной функции у = ах2 + bх + с:
1. По каким формулам можно найти координаты вершины параболы?
2. Как найти точки пересечения параболы: а) с осью абсцисс; б) с осью ординат?
3. Какое уравнение имеет ось симметрии параболы?
V. Задание на уроке
№ 621 (1, 3); 622 (1, 2); 624 (1, 3); 625 (1, 2); 626; 629; 630 (1, 3); 631 (1); 632 (1).
VI. Задание на дом
№ 621 (2, 4); 622 (3, 4); 624 (2, 4); 625 (3, 4); 627; 628; 630 (2, 4); 631 (2); 632 (2); 633.
VII. Творческие задания
1. Напишите уравнение параболы y = ax2 + bx + c, которая проходит через точку А и имеет вершину в точке В:
а) А(0; 1) и В(1; -2); б) A(0; -5) и В(3; 4); в) А(1; 2) и В(-1; -10); г) А(-1; 9) и В(-2; 11).
Ответы: а) у = 2х2 - 4х + 1; б) у = -х2 + 6х - 5; в) у = bх2 + 6х – 7; г) у = -2х2 - 8х + 3.
2. Найдите значение параметра k, при котором прямая у1 касается параболы у2. Найдите координаты точки касания:
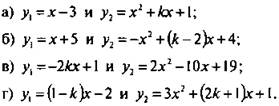
Ответы: а) при k = -3 (2; -1), при k = 5 (-2; -5);
б) при k = 1 (-1; 4), при k = 5 (1; 6);
в) при k = -1 (3; 7), при k = 11 (-3; 67);
г) при k = -2 (1; 1), при k = 2 (-1; -1).
3. Напишите уравнение параболы у = х2 + px + q, если вершина ее находится в точке А:
а) А(1; -4); б) А(-1; 5); в) А(2; -3); г) A(-4; -1).
Ответы: а) у = х2 - 2х - 3; б) y = х2 + 2х + 6; в) у = х2 - 4х + 1; г) у = -х2 - 8х - 17.
VIII. Подведение итогов урока