Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Итоги контрольной работы - урок 9 - ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ - КВАДРАТИЧНАЯ ФУНКЦИЯ
Цели: сообщить результаты работы, рассмотреть наиболее типичные ошибки, разобрать трудные задачи.
Ход урока
I. Сообщение темы и цели урока
II. Итоги контрольной работы
1. Распределение работ по вариантам и результатам решения. Данные о результатах работы удобно заносить в таблицу (для каждой пары вариантов).
№ задачи Итоги |
1 |
2 |
3 |
... |
6 |
+ |
5 |
||||
± |
1 |
||||
— |
1 |
||||
Ø |
1 |
Обозначения:
+ — число решивших задачу правильно или почти правильно.
± — число решивших задачу со значительными ошибками; .
— — число не решивших задачу;
Ø — число не решавших задачу. Вариант 1, 2 — 8 учеников.
2. Типичные ошибки, возникшие при решении задач.
3. Наиболее трудные задачи и их разбор (учителем или школьниками, сделавшими эту задачу).
4. Разбор всей контрольной работы (вывесить на стенде ответы к заданиям вариантов и разбор наиболее трудных вариантов).
III. Ответы и решения
Вариант 1
1. Ответ: -5.
2. Ответ: х1 = -6, x1 = 1.
3. Ответ: x0 = 3, у0 = 1.
4. Ответ: x = -3.
5. Ответ: у = х2 + 8х + 7.
Вариант 2
1. Ответ: -42.
2. Ответ: х1 = 1, х2 = 3.
3. Ответ: x0 = 2, у0 = -4.
4. Ответ: х = -2.
5. Ответ: у = х2 + 6х + 5.
Вариант 3
1. Ответ: у = 2х2 - 5х + 6.
2. Ответ: х1 = 1/2, х2 = 1.
3. Ответ: х0 = -1, y0 = -7.
4. Ответ-. (-2; -7), (1/3; -2).
5. Ответ: 19.
Вариант 4
1. Ответ: y = -3x2 + 22x - 34.
2. Ответ: х1 = 3/4, х2 = 1.
3. Ответ: х0 = -1, у0 = 10.
4. Ответ: (3/2; 4), (2; 6).
5. Ответ: -13.
Решения
Вариант 5
1. Для функции y(x) = -3x2 + 4x - 2 подставим значение аргумента и получим ![]()
Ответ: -3х2 + 2х - 1.
2. Так как значение функции у = х2 + 2ax - a2 равно 2а2, то получим однородное квадратное уравнение: х2 + 2ах - а2 = 2а2 или х2 + 2ах - 3а2 = 0. Решим его, используя формулу с четным вторым коэффициентом: ![]() т. е. х1 = -3 а и х2 = а. Поэтому при а ≠ 0 значение 2а2 функция достигает в двух разных точках х1 = -3а и х2 = а. При а = 0 функция достигает данного значения в одной точке х = 0.
т. е. х1 = -3 а и х2 = а. Поэтому при а ≠ 0 значение 2а2 функция достигает в двух разных точках х1 = -3а и х2 = а. При а = 0 функция достигает данного значения в одной точке х = 0.
Ответ: при а ≠ 0 x1 = -3а и x2 = а; при а = 0 x = 0.
3. Пусть первое число равно х, тогда второе число 80 - х. Найдем сумму квадратов этих чисел ![]() Функция у = 2х2 – 160x + 6400 достигает наименьшего значения при
Функция у = 2х2 – 160x + 6400 достигает наименьшего значения при ![]() Итак, если каждое из чисел равно 40, то сумма квадратов таких чисел будет наименьшей.
Итак, если каждое из чисел равно 40, то сумма квадратов таких чисел будет наименьшей.
Ответ: 40 и 40.
4. Так как значения функций равны, то получаем уравнение х2 - 3х + 4 = |5х - 3|. Для его решения раскроем знак модуля.
а) Если 5x - 3 < 0 (т. е. х < 3/5), то получаем уравнение: х2 - 3х + 4 = -(5x - 3) или х2 + 2х + 1 = 0, или (x + 1)2 = 0. Его корень х = -1 удовлетворяет условию х < 3/5 и является решением данного уравнения.
б) Если 5х – 3 ≥ 0 (т. е. х ≥ 3/5), то получаем уравнение: х2 - 3х + 4 = 5х – 3 или х2 - 8х + 7 = 0. Его корни х1 = 1 и х2 = 7 удовлетворяют условию х ≥ 3/5 и также являются решениями данного уравнения.
Ответ: х1 = -1, х2 = 1 и х3 = 7.
5. Построим график функции y = (x + 3)|x - 1|. Для этого раскроем знак модуля.
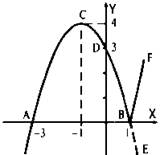
а) Если х – 1 < 0 (т. е. х < 1), то функция имеет вид у = (х + 3)(1 – x). Найдем точки пересечения параболы с осью абсцисс. Получаем уравнение 0 = (x + 3)(1 - x), корни которого х1 = -3 и х2 = 1 (точки А и В). Абсцисса вершины параболы ![]() ордината
ордината ![]() Строим вершину параболы — точку С. Найдем точку пересечения параболы с осью ординат. Положим х = 0 и получим у(0) = (0 + 3)(1 - 0) = 3 (точка D). Через точки А, В, С и D проводим параболу и выбираем ту ее часть, для которой х < 1.
Строим вершину параболы — точку С. Найдем точку пересечения параболы с осью ординат. Положим х = 0 и получим у(0) = (0 + 3)(1 - 0) = 3 (точка D). Через точки А, В, С и D проводим параболу и выбираем ту ее часть, для которой х < 1.
б) Если х – 1 ≥ 0 (т. е. х ≥ 1), то функция имеет вид y = (x + 3)(x - 1). Запишем ее в виде y = -(x + 3)(1 - x). Сравнивая ее с функцией в пункте а) y = (x + 3)(1 - x), можно увидеть, что их значения противоположны по знаку. Поэтому при х ≥ 1 участок BE уже построенной в пункте а) параболы зеркально отражаем относительно оси абсцисс и получаем кривую BF. Итак, график функции построен.
Ответ: см. график.
6. Если (х0; у0) — точка касания прямой и параболы, то (х0; у0) — единственное решение системы уравнений ![]() Приравняем правые части уравнений и получим квадратное уравнение: 2х + 3 = kх2 + 6х + 4 или 0 = kх2 + 4х + 1. Это уравнение (а следовательно, и система уравнений) имеет единственное решение, если дискриминант D = 16 – 4k = 0, откуда k = 4. При k = 4 уравнение 0 = kх2 + 4х + 1 имеет вид 0 = 42 + 4х + 1 или 0 = (2х + 1)2, откуда x = -1/2, тогда
Приравняем правые части уравнений и получим квадратное уравнение: 2х + 3 = kх2 + 6х + 4 или 0 = kх2 + 4х + 1. Это уравнение (а следовательно, и система уравнений) имеет единственное решение, если дискриминант D = 16 – 4k = 0, откуда k = 4. При k = 4 уравнение 0 = kх2 + 4х + 1 имеет вид 0 = 42 + 4х + 1 или 0 = (2х + 1)2, откуда x = -1/2, тогда ![]() Итак, при k = 4 данные прямая и парабола касаются в точке (-1/2; 2).
Итак, при k = 4 данные прямая и парабола касаются в точке (-1/2; 2).
Ответ: k = 4, (-1/2; 2).
Вариант 6
1. Для функции у(х) = 2х2 - 7х + 1 подставим значение аргумента и получим ![]()
Ответ: 8х2 - 22х + 10.
2. Так как значение функции y = x2 – ax - a2 равно a2, то получим однородное квадратное уравнение: x2 – ax - a2 = a2 или x2 – ax - 2a2 = 0. Решим его: ![]() т. е. x1 = -a и х2 = 2a. Поэтому при a ≠ 0 значение а2 функция достигает в двух разных точках х1 = -а и х2 = 2а. При а = 0 функция достигает данного значения в одной точке х = 0.
т. е. x1 = -a и х2 = 2a. Поэтому при a ≠ 0 значение а2 функция достигает в двух разных точках х1 = -а и х2 = 2а. При а = 0 функция достигает данного значения в одной точке х = 0.
Ответ: при а ≠ 0 х1 = -а и х2 = 2а; при а = 0 х = 0.
3. Пусть первое число равно х, тогда второе число 60 - х. Найдем произведение этих чисел y = x(60 - x) = -x2 + 60x. Функция y = -х2 + 60х достигает наименьшего значения при ![]() Итак, если каждое из чисел равно 30, то произведение таких чисел будет наибольшим.
Итак, если каждое из чисел равно 30, то произведение таких чисел будет наибольшим.
Ответ: 30 и 30.
4. Так как значения функций равны, то получаем уравнение х2 - 2х + 5 = |3х + 1|. Для его решения раскроем знак модуля.
а) Если 3х + 1 < 0 (т. е. x = -1/3), то получаем уравнение: х2 - 2х + 5 = -(3х + 1) или х2 + х + 6 = 0. Дискриминант уравнения отрицательный и оно корней не имеет.
б) Если 3х + 1 ≥ 0 (т. е. х ≥ -1/3), то получаем уравнение: х2 - 2х + 5 = 3х + 1 или х2 - 5х + 4 = 0. Его корни х1 = 1 и х2 = 4 удовлетворяют условию x ≥ -1/3 и являются решениями данного уравнения.
Ответ: x1 = 1, х2 = 4.
5. Построим график функции у = |х + 3|(х - 1). Для этого раскроем знак модуля.
а) Если х + 3 < 0 (т. е. х < -3), то функция имеет вид y = -(х + 3)(х – 1). Найдем точки пересечения параболы с осью абсцисс. Получаем уравнение 0 = -(х + 3)(х - 1), корни которого x1 = -3 и х2 = 1 (точки А и В). Абсцисса вершины параболы ![]() ордината
ордината ![]() Строим вершину параболы - точку С. Найдем точку пересечения параболы с осью ординат. Положим x = 0 и получим y(0) = -(0 + 3)(0 - 1)= 3 (точка D). Через точки А, В, С, D проводим параболу и выбираем ту ее часть, для которой x < -3 (часть АЕ).
Строим вершину параболы - точку С. Найдем точку пересечения параболы с осью ординат. Положим x = 0 и получим y(0) = -(0 + 3)(0 - 1)= 3 (точка D). Через точки А, В, С, D проводим параболу и выбираем ту ее часть, для которой x < -3 (часть АЕ).
б) Если х + 3 ≥ 0 (т. е. х ≥ -3), то функция имеет вид y = (x + 3)(x - 1). Сравнивая ее с функцией в пункте а) у = -(x + 3)(x - 1), можно увидеть, что их значения противоположны по знаку. Поэтому при x ≥ -3 участок ACDBF уже построенной в пункте а) параболы зеркально отражаем относительно оси абсцисс и получаем кривую AHBG.
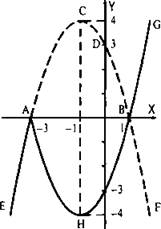
Итак, график функции построен.
Ответ: см. график.
6. Если (х0; у0) — точка касания прямой и параболы, то (x0; у0) — единственное решение системы уравнений ![]() Приравняем правые части уравнений и получим квадратное уравнение: 3х - 2 = kх2 - 3х - 1 или 0 = kх2 – 6x + 1. Эго уравнение (а следовательно, и система уравнений) имеет единственное решение, если дискриминант D = 36 – 4k = 0, откуда k — 9. При k = 9 уравнение 0 = kx2 - 6х + 1 имеет вид 0 = 9x2 – 6x + 1 или 0 = (3x - 1)2, откуда х = 1/3, тогда
Приравняем правые части уравнений и получим квадратное уравнение: 3х - 2 = kх2 - 3х - 1 или 0 = kх2 – 6x + 1. Эго уравнение (а следовательно, и система уравнений) имеет единственное решение, если дискриминант D = 36 – 4k = 0, откуда k — 9. При k = 9 уравнение 0 = kx2 - 6х + 1 имеет вид 0 = 9x2 – 6x + 1 или 0 = (3x - 1)2, откуда х = 1/3, тогда ![]() Итак, при k = 9 данные прямая и парабола касаются в точке (1/3; -1).
Итак, при k = 9 данные прямая и парабола касаются в точке (1/3; -1).
Ответ: k = 9, (1/3; -1).