ПОВТОРЕНИЕ: ЧИСЛОВЫЕ И АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ

Цели: повторить правила выполнения действий с обыкновенными и десятичными дробями, понятие процента, понятие и свойства степени, правила выполнения действий с одночленами и многочленами; рассмотреть решение заданий повышенной трудности и нестандартных заданий.

Ход урока

I. Организационный момент.

Вступительное слово учителя.

II. Решение задач.

1) Повторить правила выполнения действий с десятичными дробями, вычислив рациональным способом:

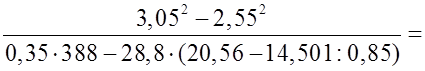
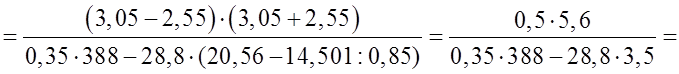
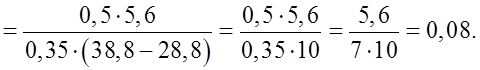
Вспомнить правила выполнения действий с обыкновенными дробями:

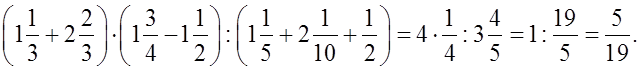
Рассмотреть решение примеров, в которых встречаются и десятичные и обыкновенные дроби.

а)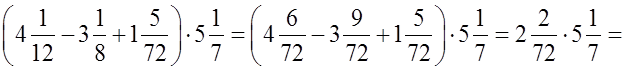

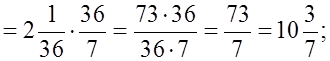
б)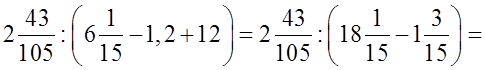

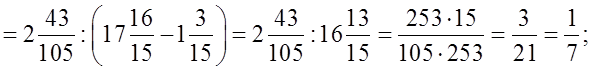
в)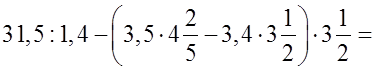

= 22,5 – (3,5 ⋅ 4,4 – 3,4 ⋅ 3,5) ⋅ 3,5 = 22,5 – 3,5 (4,4 – 3,4) ⋅ 3,5 = 22,5 – 3,5 ⋅ 3,5 = 22,5 – 12,25 = 10,25;

г)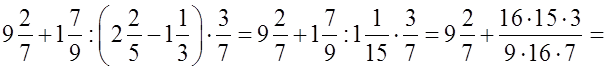

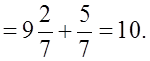
2) Повторить определение процента, правила перевода десятичной дроби в процент и процента в десятичную дробь, правила нахождения процента от числа и нахождение числа по его проценту.

Затем рассмотреть решение задачи:

В результате инфляции цену товара увеличили на 25 %. В связи с низким спросом цену товара снизили на 10 %. На сколько процентов последняя цена стала больше первоначальной?

3) Повторить определение степени, её свойства, записать их на доске и в тетрадях.

Рассмотреть решение более сложных заданий на данную тему:

а) 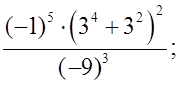б)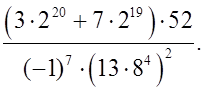

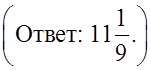
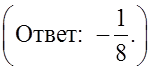
Сильным учащимся можно предложить решение следующих заданий:

а) определите, делится ли выражение 810 – 89 – 88 на 55;

б) определите, делится ли выражение 128 ⋅ 912 на 616.

4) Вспомнить понятия одночленов и многочленов, повторить правила выполнения действий с ними.

Сильным учащимся предлагается задание:

а) Какое наименьшее целое число надо прибавить к произведению (x – 3)(x – 7), чтобы оно стало положительным при любом x?

б) Чему равно (a + b)3, если имеет место следующее равенство a2 – 4a + 5 + b2 = 0?

Закрепить навык разложения многочленов на множители.

III. Подведение итогов.

Домашнее задание.

ПОВТОРЕНИЕ: ЧИСЛОВЫЕ И АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ

Цели: повторить правила выполнения действий с обыкновенными и десятичными дробями, понятие процента, понятие и свойства степени, правила выполнения действий с одночленами и многочленами; рассмотреть решение заданий повышенной трудности и нестандартных заданий.

Ход урока

I. Организационный момент.

Вступительное слово учителя.

II. Решение задач.

1) Повторить правила выполнения действий с десятичными дробями, вычислив рациональным способом:

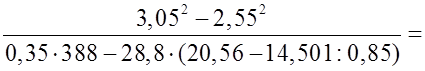
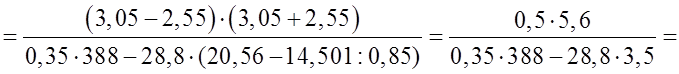
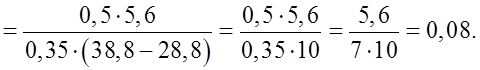
Вспомнить правила выполнения действий с обыкновенными дробями:

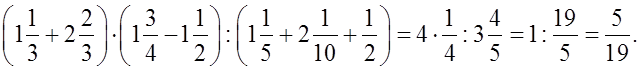
Рассмотреть решение примеров, в которых встречаются и десятичные и обыкновенные дроби.

а)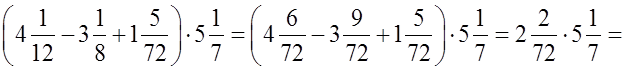

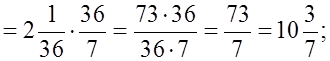
б)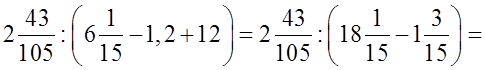

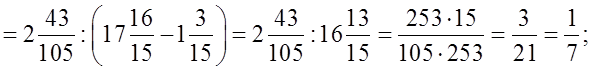
в)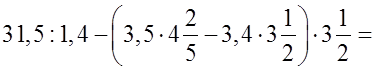

= 22,5 – (3,5 ⋅ 4,4 – 3,4 ⋅ 3,5) ⋅ 3,5 = 22,5 – 3,5 (4,4 – 3,4) ⋅ 3,5 = 22,5 – 3,5 ⋅ 3,5 = 22,5 – 12,25 = 10,25;

г)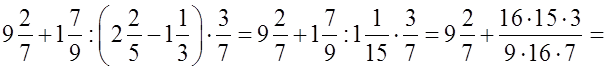

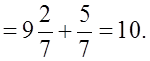
2) Повторить определение процента, правила перевода десятичной дроби в процент и процента в десятичную дробь, правила нахождения процента от числа и нахождение числа по его проценту.

Затем рассмотреть решение задачи:

В результате инфляции цену товара увеличили на 25 %. В связи с низким спросом цену товара снизили на 10 %. На сколько процентов последняя цена стала больше первоначальной?

3) Повторить определение степени, её свойства, записать их на доске и в тетрадях.

Рассмотреть решение более сложных заданий на данную тему:

а) 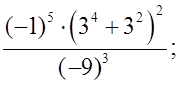б)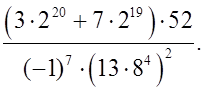

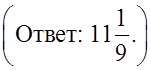
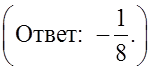
Сильным учащимся можно предложить решение следующих заданий:

а) определите, делится ли выражение 810 – 89 – 88 на 55;

б) определите, делится ли выражение 128 ⋅ 912 на 616.

4) Вспомнить понятия одночленов и многочленов, повторить правила выполнения действий с ними.

Сильным учащимся предлагается задание:

а) Какое наименьшее целое число надо прибавить к произведению (x – 3)(x – 7), чтобы оно стало положительным при любом x?

б) Чему равно (a + b)3, если имеет место следующее равенство a2 – 4a + 5 + b2 = 0?

Закрепить навык разложения многочленов на множители.

III. Подведение итогов.

Домашнее задание.