Поурочные разработки по Алгебре 8 класс
ПЕРВЫЕ ПРЕДСТАВЛЕНИЯ О РЕШЕНИИ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ
Цели: повторить правила решения линейных уравнений; объяснить правила решения рациональных уравнений; формировать умение решать уравнения.
Ход урока
I. Организационный момент.
II. Анализ самостоятельной работы.
Выставить оценки за самостоятельную работу. На доске разобрать задания, которые вызвали затруднения при решении, обязательно разобрать задания № 6.10 с полным объяснением.
Задание № 6.10.
а) Доказать тождество 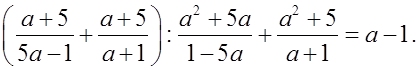
Р е ш е н и е:
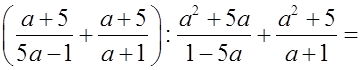
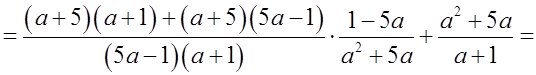
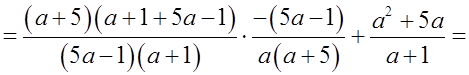
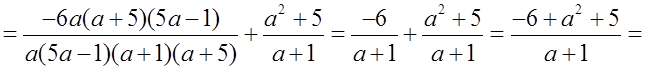
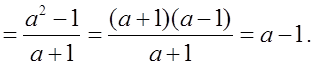
О т в е т: a – 1 = a – 1.
б) Доказать тождество 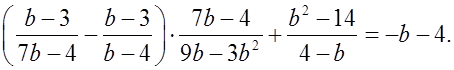
Р е ш е н и е:
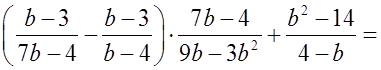
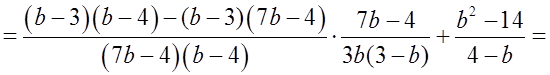
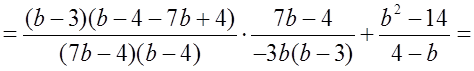
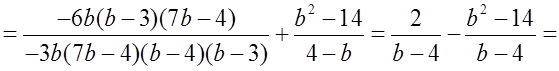
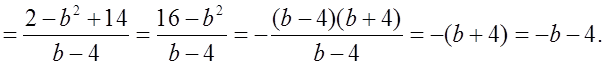
О т в е т: – b – 4.
Учащимся, не справившимся с самостоятельной работой предлагается дополнительная домашняя самостоятельная работа.
Выполнить следующие действия:
1) 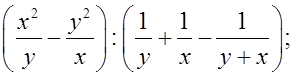
2) 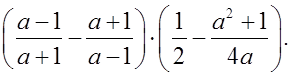
III. Объяснение нового материала.
Учащимся предлагается ответить на следующие вопросы:
– Какое выражение называется рациональным? Привести пример рационального алгебраического выражения.
– В каком случае дробь не имеет смысла? Что называется областью допустимых значений дроби.
– Каково условие равенства алгебраической дроби нулю?
Далее учитель вводит определение рационального уравнения. На примерах разбираются способы решения уравнений.
Первое и второе уравнения на доске решают учащиеся, комментируя каждый этап (учитель только помогает). Решение третьего уравнения лучше выполнить учителю с привлечением учащихся.
1) 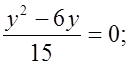
2) 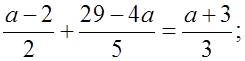
3) 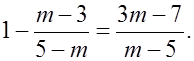
1) Преобразуем данное уравнение.
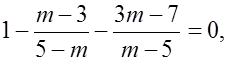
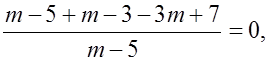
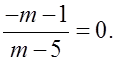
2) Дробь обращается в нуль лишь при условиях, что числитель равен 0, а знаменатель отличен от нуля.
Значит, –m – 1 = 0; m = –1.
При m = –1, знаменатель m – 5 = –1 – 5 = – 6 0.
О т в е т: m = –1.
IV. Закрепление нового материала.
1) Решить уравнения № 7.8; 7.12; 7.28.
2) В классах с сильными учащимися предлагается разобрать решение следующих уравнений:
а) 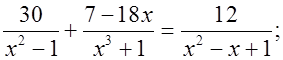
б) 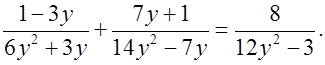
V. Подведение итогов.
Домашнее задание: изучить материал параграфа 7, выучить правила. Решить задачи № 7.5; 7.14; 7.29.