Поурочные разработки по Алгебре 8 класс
Урок 1 - ФУНКЦИЯ y = kx2, ЕЕ СВОЙСТВА И ГРАФИК
Цели: провести анализ контрольной работы; вспомнить свойства функций y = kx + b и y = x2, их графики; объяснить свойства функции y = kx2 и показать построение графика данной функции; формировать умение строить графики функций y = kx + b и y = kx2, и по графику определять свойства данных функций.
Ход урока
I. Организационный момент.
II. Анализ контрольной работы.
Выставить оценки за контрольную работу. Разобрать задания, с которыми не справилось большинство учащихся.
В а р и а н т 1
5*. Упростить выражение:
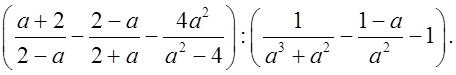
Р е ш е н и е:
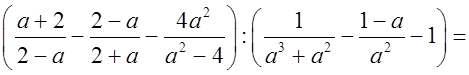
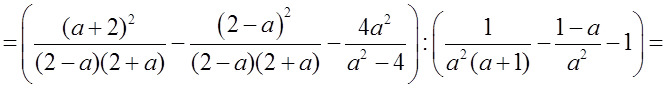
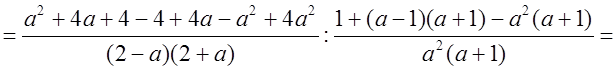
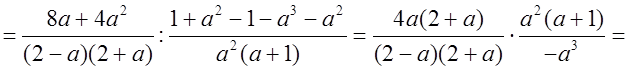
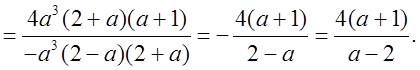
О т в е т: 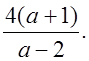
В а р и а н т 2
5*. Упростить выражение:
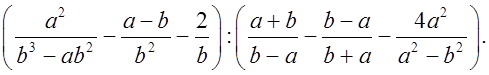
Р е ш е н и е:
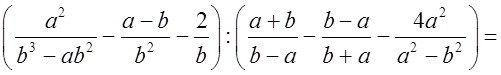
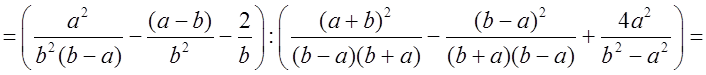
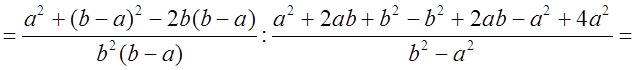
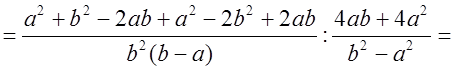
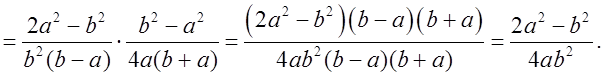
О т в е т: 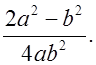
III. Актуализация знаний.
1) Повторить понятие линейной функции, её свойства и построение графика данной функции. Закрепить знания о том, что графиком линейной функции является прямая, для построения которой необходимы координаты двух точек, а свойства зависят от коэффициента k.
На доске разобрать построение графика функции
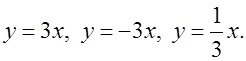
По графику функции определить свойства.
2) Повторить построение графика функции y = x2.
IV. Объяснение нового материала.
На доске, на координатной плоскости пунктирной линией построить график функции y = x2 и сплошной линей графики функций y = 3x2, y = –3x2 и 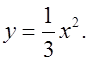 После этого вместе с учащимися сделать выводы.
После этого вместе с учащимися сделать выводы.
Если коэффициент перед переменной x больше 1, то график функции y = kx2 круче графика функции y = x2. Если коэффициент меньше 1, то график функции y = x2 круче графика функции y = kx2. Если же коэффициент является отрицательным числом, то ветви параболы направлены вниз.
Затем учитель показывает общую схему построения графиков функций y = kx2, если k > 1 и 0 < k < 1.
Записываются свойства данной функции при данных условиях учителем на доске, учениками в тетрадях.
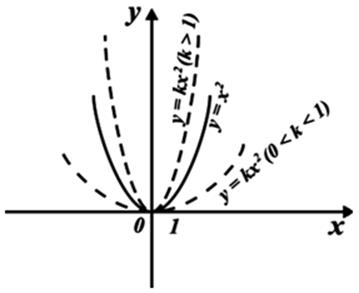
1. Область определения (–; +).
2. у = 0 при х = 0, у > 0 при х 0.
3. y = kx2 является непрерывной функцией (понятие непрерывности рассматривается только на графике – сплошная линия).
4. ymin = 0 при х = 0; ymax не существует.
5. Возрастает данная функция y = kx2 при x ≥ 0; убывает при x ≤ 0.
6. Данная функция ограничена снизу и не ограничена сверху.
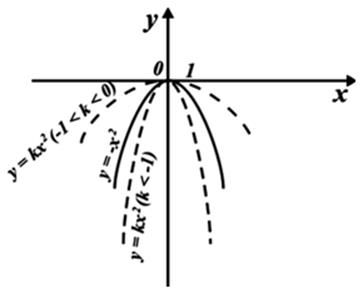
Затем учитель показывает общую схему построения графиков функции y = kx2 при значениях –1 < k < 0 и k < –1.
Учащиеся самостоятельно записывают свойства функции y = kx2 при заданном условии k < 0. Затем следует проверка.
V. Закрепление нового материала.
1) Схематично изобразить графики данных функций относительно графика y = x2 : y = 6x2, y = –2x2, y = 2x2, 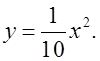
2) Разобрать задания № 17.4 (г); 17.5 (г); 17.15; 17.16; 17.20; 17.23; 17.24.
VI. Подведение итогов.
Домашнее задание: прочитать материал параграфа 17, выучить правила. Решить задачи № 17.3; 17.4 (г); 17.25.