Урок 2 - ФУНКЦИЯ y = kx2, ЕЕ СВОЙСТВА И ГРАФИК

Цели: закрепить знания о свойствах функции вида y = kx2 и умение строить ее график; ввести правила решения уравнений графическим способом; показать способ построения графиков функций, заданных несколькими условиями; развивать умение строить графики известных функций.

Ход урока

I. Организационный момент.

II. Индивидуальная работа.

К доске для самостоятельного выполнения заданий вызываются четыре ученика.

Карточка 1

Построить на координатной плоскости график функции y = 4x2, найти наибольшее значение данной функции на отрезке [–1; 1]. Сформулировать свойства данной функции.

Карточка 2

Построить на координатной плоскости график функции y = –3x2, найти наименьшее значение данной функции на интервале [–1; 1). Сформулировать свойства данной функции.

Карточка 3

Построить на координатной плоскости график функции 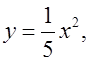найти наименьшее значение данной функции на интервале [0; +). Сформулировать свойства данной функции.

Карточка 4

Построить на координатной плоскости график функции y = –0,4x2, найти наименьшее значение данной функции на интервале (–; 0]. Сформулировать свойства данной функции.

III. Актуализация знаний.

Во время выполнения индивидуальной работы остальные учащиеся класса проверяют домашнее задание.

Затем устно выполняются задания № 17.1; 17.6; 17.7; 17.19; 17.21. При наличии времени можно выполнить задание № 17.24.

Индивидуальные задания проверяются всем классом.

IV. Объяснение нового материала.

1) Учитель на доске показывает графическое решение уравнения x2 = 3x – 2.

Р е ш е н и е:

Для графического решения данного уравнения необходимо построить графики функций y = x2 и y = 3x – 2 на одной координатной плоскости.

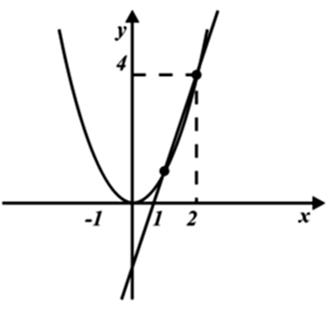
Графиком функции y = x2 является парабола, с вершиной в точке (0; 0). Ветви параболы направлены вверх. Парабола проходит через точки (1; 1), (–1; 1), (2; 4), (–2; 4).

Графиком функции y = 3x – 2 является прямая. Для построения прямой необходимы координаты двух точек. Для данной функции это точки: (1; 1), (0; –2).

Теперь строятся графики.

Графики данных функций имеют точки пересечения (1; 1) и (2; 4). Решением заданного уравнения являются абсциссы точек пересечения – числа 1 и 2.

О т в е т: 1; 2.

2) Один из сильных учеников класса, с помощью учителя, показывает на доске графическое решение системы уравнений

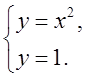
3) Строится график кусочной функции y = f(x), где:

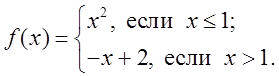
V. Закрепление нового материала.

Решаются задания № 17.28 (а, г), 17.31; 17.43; 17.35 (а, б).

С сильными учащимися при наличии времени разбирается решение задания № 17.62.

VI. Подведение итогов.

Домашнее задание: рассмотреть примеры решения из учебника. Решить задачи № 17.28 (б); 17.30; 17.43; 17.35 (в, г).