Урок 2 - ОСНОВНЫЕ ПОНЯТИЯ - урок 4

Цели: повторить понятия квадратного уравнения, корня квадратного уравнения; рассмотреть решение уравнений различного уровня сложности; развивать у учащихся умение решать квадратные уравнения.

Ход урока

I. Организационный момент.

II. Индивидуальная работа.

К доске вызываются четыре ученика для самостоятельного решения заданий с карточек.

Карточка 1

Из данных уравнений выбрать квадратные, определить их коэффициенты и вид уравнения:

а) 2x2 – 3 + x = 0; б) 3x2 + 4 = 0;

в) 7x – x2 = 0; г) –x2 + x – 1 = 0;

д) x + 2 = 0; е) x3 + 3 – 3 = 0.

Карточка 2

Привести данные уравнения к стандартному виду: ax2 + bx + c = 0.

а) x(2x – 1) + 3(x – 2) = 0;

б) (x – 2)(3 – 4x) + 4x(x – 5) = 0.

Карточка 3

Для какого из данных уравнений корнями являются числа – 1, 3, 2:

а) x2 – 4x + 3 = 0; б) 5x – x2 – 6 = 0; в) x2 – 5x + 6 = 0.

Карточка 4

Решить уравнения:

а) x2 – 49 = 0; б) x2 – 9x = 0; в) 2x2 + 50 = 0.

III. Актуализация знаний.

Пока у доски проходит индивидуальная работа, остальные учащиеся самостоятельно выполняют задание № 24.6.

Затем проверяется домашнее задание, задания из тетради и задания, решенные на доске. После этого всем классом устно выполняются задания № 24.1; 24.10; 24.11.

IV. Решение задач.

Повторяются ранее известные способы решения квадратных уравнений на конкретных примерах (7 способов).

x2 + 4x + 3 = 0

1) Графический способ.

а) Построим график функции x2 + 4x + 3 = 0. Корнями уравнения x2 + 4x + 3 = 0 служат абсциссы точки пересечения с осью Ох: (–3; 0); (–1; 0).

Итак: х1 = –3; х2 = –1.

б) Преобразуем уравнение x2 = –4x – 3. Построим в одной системе координат графики функций y = x2 и y = –4x – 3.

Они пересекаются в точках А (–1; 1), В (–3; 9), х1 = –3; х2 = –1.

в) Преобразуем уравнение x2 + 3 = –4x. Построим графики функций y = x2 + 3 и y = –4x.

Найдем абсциссы точек пересечения.

г) Преобразуем уравнение к виду:

x2 + 4x + 4 – 4 + 3 = 0;

(x + 2) 2 – 1 = 0;

(x + 2) 2 = 0.

Построим в одной системе координат графики и у = (x + 2) 2 и у = 1 найдем абсциссы точек пересечения.

д) Разделим обе части уравнения на:

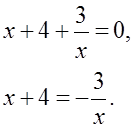
Построим в одной системе координат графики функции у = х + 4 и 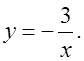Найдем абсциссы точек пересечения.

2) Аналитический способ.

Используется два способа разложения на множители:

а) выделение полного квадрата

x2 + 4x + 3 = 0;

x2 + 4x + 4 – 4 + 3 = 0;

(x + 2)2 – 1 = 0;

(x + 2 – 1) (x + 2 + 1) = 0;

(x + 1) (x + 3) = 0;

x + 1 = 0 или x + 3 = 0;

x = –1 или x = – 3.

б) x2 + 4x + 3 = 0;

x2 + 3x + х + 3 = 0;

х(x + 3) + (x + 3) = 0;

(x + 3) (x + 1) = 0;

x + 3 = 0 или x + 1 = 0;

x = –3 или x = – 1.

1) Разобрать решения заданий № 24.24; 24.26; 24.31; 24.34.

2) С сильными учащимися разобрать решение уравнения методом введения новой переменной:

2(3x – 5) 2 = 9(3x – 5);

t = 3x – 5; 2t2 = 9t;

2t2 – 9t = 0;

t(2t – 9) = 0;

t1 = 0; t2 = 4,5.

При t = 0;

3x – 5 = 0;

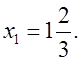
При t = 4,5;

3x – 5 = 4,5;

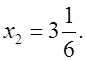
О т в е т: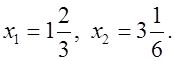

Разобрать аналогичным способом решения следующих уравнений:

а) (2x – 1) 2 = 2 – 4x; б) 4 – 9(2 – 5x) 2 = 0.

V. Подведение итогов.

Домашнее задание: решить задания № 24.25; 24.33.