Урок 2 - РЕШЕНИЕ ЛИНЕЙНЫХ НЕРАВЕНСТВ

Цели: повторить правила решения линейных неравенств; рассмотреть решение линейных неравенств различного уровня сложности; развивать умение решать неравенства и показывать решение на координатной прямой.

Ход урока

I. Организационный момент.

II. Индивидуальная работа.

К доске вызываются четыре ученика, которые самостоятельно выполняют задания с карточек:

Карточка 1 Из данных чисел 2, 5, –7 выберите числа, которые являются решением неравенства 2x + 1 > 7 – x.	Карточка 2 Решите неравенство и решение покажите на координатной прямой: 3x < 21.
Карточка 3 Решите неравенство и изобразите множество решений на координатной прямой: 5x > –20.	Карточка 4 При каких значениях x двучлен 5x – 7 принимает положительные значения?

III. Актуализация знаний.

Во время проведения индивидуальной работы остальные учащиеся устно решают следующие неравенства:

2x > 24; 5x < –15; –3x > 21; 10x < –30; –2x < –16.

Затем выполняют № 33.2; 33.12; 33.25 (б).

IV. Решение задач.

1) Решаются неравенства № 33.15; 33.17; 33.19; 33.21; 33.30 (а, б).

2) Найдите наибольшее целое значение переменной x, удовлетворяющей неравенству:

а) 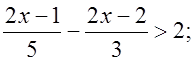б)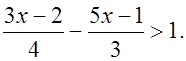

3) Найдите наименьшее целое x, удовлетворяющее неравенству:

а) 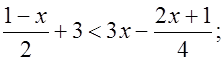б)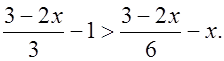

4) С сильными учениками разобрать решение следующего неравенства:

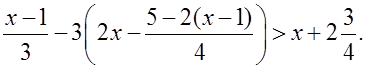
Р е ш е н и е:

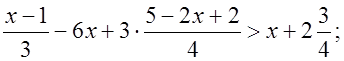
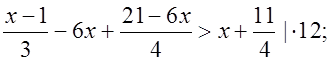
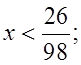
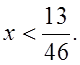
О т в е т: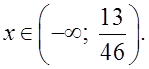

V. Подведение итогов.

Домашнее задание: решить задачи № 33.16; 33.18; 33.23; 33.25 (в).