Системы неравенств с двумя переменными - Неравенства с двумя переменными и их системы - Уравнения и неравенства с двумя переменными

Цель: построение решения системы неравенств с двумя переменными на координатной плоскости.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

Изобразите на координатной плоскости множество точек, задаваемых неравенством.

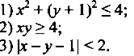
Вариант 2

Изобразите на координатной плоскости множество точек, задаваемых неравенством.

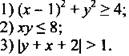
III. Изучение нового материала

В ряде случаев на координатной плоскости приходится изображать множество решений системы неравенств с двумя переменными. Напомним, что пара значений неизвестных, которая одновременно является решением и первого и второго неравенства, называется решением системы двух неравенств с двумя переменными.

Пример 1

Рассмотрим систему неравенств с двумя переменными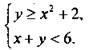

Пара значений переменных (1; 4) является решением системы неравенств, т. к. является решением каждого неравенства: 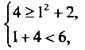или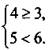

Пара значений переменных (1; 1) не является решением системы неравенств, т. к. не является решением первого неравенства: 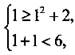или

Множеством решений системы неравенств с двумя переменными является пересечение множеств решений всех неравенств, входящих в систему. На координатной плоскости множество решений системы неравенств изображается множеством точек, являющихся общей частью множеств, представляющих собой решения каждого неравенства системы.

Пример 2

Изобразим на координатной плоскости множество решений системы неравенств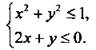

Первое неравенство системы задает на координатной плоскости круг с центром в начале координат и радиусом, равным 1. Второе неравенство задает полуплоскость, расположенную ниже прямой 2х + у = 0.

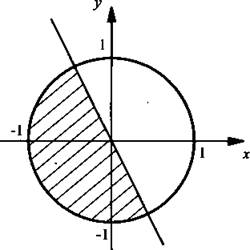
Итак, решениями данной системы неравенств являются точки полукруга (они заштрихованы).

Пример 3

На плоскости х0у изобразим точки, удовлетворяющие системе неравенств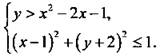

Изобразим сначала точки, удовлетворяющие первому неравенству. Построим график границы - график функции у = х2 - 2х - 1. Эта парабола пересекает ось 0у в точке у = -1, ось 0х в точках Вершина параболы находится в точке (1; -2), ветви параболы направлены вверх. Эта кривая разбила координатную плоскость на часть, заключенную между ветвями параболы, и часть, находящуюся за ветвями параболы. Взяв любую точку, например (1; -1), из первой части плоскости, видим, что она удовлетворяет неравенству у > х2 - 2х - 1. Поэтому все точки этой части также удовлетворяют неравенству (за исключением границы, т. к. неравенство строгое).

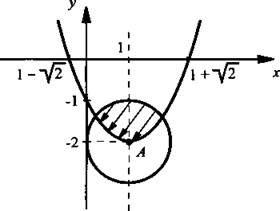
Аналогично, построив границу (х - 1)2 + (у + 2)2 = 1, видим, что неравенству (х - 1)2 + (у + 2)2 ≤ 1 удовлетворяют внутренние и граничные точки окружности.

Штриховкой показаны те точки, которые удовлетворяют системе неравенств. Причем стрелки показывают, что данная граница (часть параболы) не входит в множество решений системы неравенств.

Пример 4

Изобразим множество точек, которые являются решениями системы неравенств 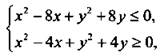и вычислим площадь этой фигуры.

Запишем систему неравенств в следующем виде: 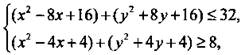или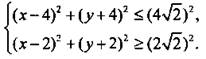

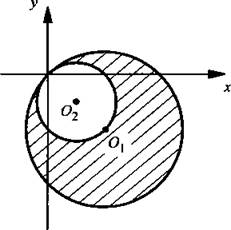
Графиком первого неравенства является круг с центром в точке O1(4; -4) и радиусом Графиком второго неравенства являются точки, расположенные за окружностью с центром в точке O2(2; -2) и радиусом Итак, решениями данной системы неравенств являются точки, расположенные между двумя касающимися в начале системы координат окружностями (эти точки заштрихованы).

Найдем площадь этой фигуры. Она равна разности площадей окружностей: Таким образом, площадь заштрихованной фигуры ровно в 3 раза больше площади малого круга.

IV. Задание на уроке

№ 496 (а, б); 497 (б, г); 498 (а); 499 (б); 500 (а, в); 501 (а); 502 (б); 503.

V. Задание на дом

№ 496 (в, г); 497 (а, в); 498 (в); 499 (а); 500 (б, г); 501 (б); 502 (а).

VI. Подведение итогов урока