Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии - Арифметическая прогрессия - Арифметическая и геометрическая прогрессии

Цель: рассмотреть частный вид последовательности - арифметическую прогрессию.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Определение возрастающей последовательности.

2. Последовательность (аn) задана формулой Найдите a1, a5, a10.

3. Последовательность (аn) задана формулой аn+1 = 3 - 2аn, где a1 = 2 и n ≥ 1. Найдите первые четыре члена последовательности.

Вариант 2

1. Определение убывающей последовательности.

2. Последовательность (аn) задана формулой Найдите a1, a5, a10.

3. Последовательность (аn) задана формулой an+1 = 3аn - 2, где a1 = 2 и n ≥ 1. Найдите первые четыре члена последовательности.

III. Изучение нового материала

Из всех последовательностей наиболее изучены две: арифметическая и геометрическая прогрессии, которые будут рассмотрены в этой главе. Сначала рассмотрим арифметическую прогрессию.

Последовательность чисел аn, каждый член которой (начиная со второго) равен предыдущему, сложенному с одним и тем же числом d (разностью прогрессии), называется арифметической прогрессией: an+1 = аn + d (n ≥ 1). При d > 0 арифметическая прогрессия возрастает, при d < 0 - убывает.

Пример 1

Найти первые пять членов арифметической прогрессии, если а1 = 5, d = 2.

Из определения арифметической прогрессии аn+1 = аn + d получаем: при n = 1 a2 = a1 + d = 5 + 2 = 7, при n = 2 a3 = a2 + d = 7 + 2 = 9, при n = 3 a4 = a2 + d = 9 + 2 = 11, при n = 4 a5 = a4 + d = 11 + 2 = 13.

Итак, эти члены: 5, 7, 11, 13.

В определении арифметической прогрессии использована рекуррентная формула an+1 = аn + d. Удобнее получить формулу n-го члена.

Пример 2

Получим формулу n-го члена арифметической прогрессии.

Из определения арифметической прогрессии ak+1 = ak + d запишем (n - 1) равенство: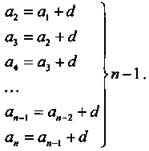

Сложим эти равенства, тогда в левой и правой части сокращаются одинаковые члены а2, a3, ..., аn-1 и получаем:

Таким образом, получена важнейшая формула - формула n-го члена арифметической прогрессии: an = a1 + d(n - 1).

Как правило, задачи на эту тему достаточно простые. Наиболее распространенный прием решения таких задач - записать условие задачи, используя в качестве неизвестной первый член и разность прогрессии.

Пример 3

В арифметической прогрессии сумма второго и пятого членов равна 8, а третьего и седьмого равна 14. Найти прогрессию.

Выразим все члены прогрессии через ее первый член и разность: а2 = а1 + d, а5 = а1 + 4d, а3 = а1 + 2d, а7 = а1 + 6d и запишем условия задачи: 8 = а1 + а5 = (a1 + d) + (а1 + 4d) = 2a1 + 5d, 14 = a3 + a7 = 2a1 + 8d.

Для определения a1 и d получаем линейную систему уравнений 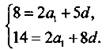Вычитая из второго уравнения первое, найдем 6 - 3d, или d = 2, и из любого из уравнений: а1 = -1.

Пример 4

Первый член арифметической прогрессии а1, а2, а3, ... равен единице. При каком значении разности прогрессии d величина S = а1а3 + а2а3 имеет минимальное значение?

Как и в предыдущей задаче, выразим члены прогрессии а2 и а3 через первый член (a1 = 1) и разность d: а2 = а1 + d = 1 + d, a3 = а1 + 2d = 1 + 2d.

Тогда S = 1(1 + 2d) + 1(1 + d)(1 + 2d) = 2d2 + 5d + 2. Функция S в зависимости от d является квадратичной функцией (параболой) и достигает минимального значения при

Пример 5

Найти сумму чисел

Обратим внимание на то, что числа, стоящие под радикалами, образуют арифметическую прогрессию: 100, 101, 102, 103, ..., 399, 400.

Умножим числители и знаменатели дробей на разность чисел, стоящих в знаменателях: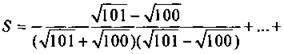

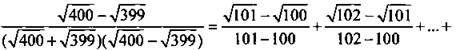
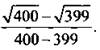
За счет того что числа образовали арифметическую прогрессию, знаменатели дробей оказались равными разности прогрессии, т. е. 1. Тогда имеем: Легко заметить, что в данной сумме сокращаются все числа, кроме и тогда сумма

Достаточно часто арифметическая прогрессия встречается в текстовых и геометрических задачах.

Пример 6

Четыре целых различных числа образуют арифметическую прогрессию. Одно из этих чисел равно сумме квадратов остальных трех чисел. Найти эти числа.

Пусть эти числа имеют вид: a; а + d; а + 2d, а + 3d (очевидно, что a и d - целые числа). Запишем условие задачи: а2 + (а + d)2 + (a + 2d)2 = а + 3d, или 3а2 + 6ad + 5d2 = а + 3d. Будем рассматривать это уравнение как квадратное, считая а неизвестной и d параметром.

Запишем уравнение в виде 3а2 + а(6d - 1) + (5d2 - 3d) = 0.

Чтобы это уравнение имело решение, необходима неотрицательность его дискриминанта D. Найдем D = (6d - 1)2 – 4 · 3 · (5d2 - 3d) = 36d2 - 12d + 1 – 60d2 + 36d = -24d2 + 24d + 1 ≥ 0.

Решим это квадратное неравенство. Корни соответствующего уравнения т. е. d1 ≈ -0,04 и d2 ≈ 1,04. Тогда решение неравенства: -0,04 ≤ d ≤ 1,04. В этом промежутке есть два целых значения d = 1 и d = 0 (не подходит, т. к. даны различные числа).

Для d = 1 уравнение 3а2 + a(6d - 1) + (5d2 - 3d) - 0 принимает вид: 3а2 + 5а + 2 = 0. Корни его: а1 = -1, а2 = -2/3 (не подходит). Итак, искомые числа: -1; 0; 1; 2.

Пример 7

Стороны четырехугольника образуют арифметическую прогрессию. Можно ли в него вписать окружность?

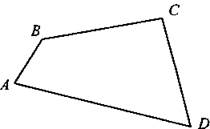
Пусть стороны четырехугольника АВ, ВС, AD, CD в указанном порядке образуют арифметическую прогрессию с первым членом а и разностью d: АВ = а, ВС = а + d, AD = а + 2d, CD = a + 3d.

В четырехугольник можно вписать окружность, если суммы его противоположных сторон равны, т. е. АВ + CD = ВС + AD. Проверим это условие: а + (а + 3d) = (а + d) + (а + 2d).

Так как равенство верное, то в такой четырехугольник можно вписать окружность. Но это возможно только в том случае, когда стороны четырехугольника образуют арифметическую прогрессию именно в следующем порядке: АВ, ВС, AD, CD.

Пример 8

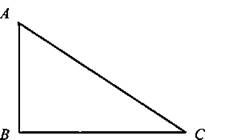
Стороны прямоугольного треугольника образуют арифметическую прогрессию. Найти стороны треугольника.

Пусть наименьший катет ΔАВС: АВ = а, тогда второй катет ВС = а + d и гипотенуза АС = а + 2d (где d - разность прогрессии, d > 0).

Запишем теорему Пифагора: АС2 = АВ2 + ВС2, или (a + 2d)2 = a2 + (а + d)2, или а2 - 2ad - 3d2 = 0.

Решая это однородное уравнение, получим: а = 3d и а = -d (не подходит). Имеем: АВ = 3d, ВС = 4d, АС = 5d (где d - любое число). Значит, условию задачи удовлетворяют прямоугольные треугольники, подобные египетскому.

Отметим еще одно важное свойство членов арифметической прогрессии. Любой член прогрессии (начиная со второго) равен полусумме соседних членов: (n ≥ 2) (характеристическое свойство).

Пример 9

Докажем характеристическое свойство арифметической прогрессии.

Используя определение арифметической прогрессии, получим:

Достаточно часто при решении задач рассматриваемой темы используется характеристическое свойство арифметической прогрессии.

Пример 10

При каких значениях х числа 6, х2, х образуют в указанном порядке арифметическую прогрессию? Найти эти числа.

Запишем свойство арифметической прогрессии: 2х2 = 6 + х. Получаем квадратное уравнение, корни которого х = -3/2 и х = 2. Тогда искомыми числами будут: 6; 9/4; или 6; 4; 2.

IV. Контрольные вопросы

1. Определение арифметической прогрессии.

2. Формула n-го члена арифметической прогрессии.

3. Характеристическое свойство арифметической профессии.

V. Задание на уроке

№ 575 (а, б); 576 (а, в, д); 577 (б); 580 (а); 581; 583; 584 (б); 587; 589 (а); 591; 593; 595; 597 (а, б, г).

VI. Задание на дом

№ 575 (в, г); 576 (б, г, е); 577 (а); 580 (б); 582; 584 (а); 588; 589 (б); 590; 592; 594; 596; 597 (в, д, е); 598.

VII. Подведение итогов урока