Формула суммы первых n членов арифметической прогрессии - Арифметическая прогрессия - Арифметическая и геометрическая прогрессии

Цель: найти сумму членов арифметической прогрессии.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Рекуррентная формула члена арифметической прогрессии.

2. Арифметическая прогрессия задана формулой аn = 3n - 5. Найдите а5 и a25.

3. В арифметической прогрессии a3 = 7 и а5 = 1. Найдите а17.

Вариант 2

1. Формула n-го члена арифметической прогрессии.

2. Арифметическая прогрессия задана формулой an = 1 – 4n. Найдите а10 и a30.

3. В арифметической прогрессии a7 = 2 и a10 = 11. Найдите а19.

III. Изучение нового материала

Сумму первых n членов арифметической профессии можно найти по формуле

Пример 1

Получим формулы суммы первых n членов арифметической прогрессии.

Обозначим сумму первых n членов арифметической прогрессии (an) через Sn. Запишем эту сумму дважды, расположив в первом случае члены в порядке возрастания их номеров, во втором случае - в порядке убывания номеров:

Сложим эти равенства:

Покажем, что все суммы в скобках равны друг другу. Получаем:

и т. д.

Тогда имеем 2Sn = (а1 + an)n, откуда (первая формула получена).

Используем формулу n-го члена an = a1 + d(n - 1). Тогда имеем: (вторая формула получена).

Пример 2

В арифметической прогрессии а3 = 7 и а8 = 27. Найдем сумму первых сорока членов прогрессии.

Сначала найдем первый член а1 и разность d прогрессии. Запишем условия задачи: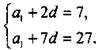

Из этой линейной системы уравнений находим а, = -1 и d = 4. Теперь найдем сумму первых сорока членов прогрессии:

Пример 3

Найти сумму всех трехзначных чисел, которые при делении на 4 дают остаток 3.

Первое число легко угадать: а1 = 103. Легко также угадать несколько последующих таких чисел: а2 = 107, a3 = 111, а4 = 115. Видно, что искомые числа образуют арифметическую прогрессию с первым членом 103 и разностью 4. Общий член этой прогрессии можно записать в виде an = 103 + 4(n - 1) = 99 + 4n.

Определим теперь число членов в сумме.

Так как последнее трехзначное число 999, то получаем условие аn ≤ 999, или 99 + 4n ≤ 999. Решив это неравенство, найдем n ≤ 225.

Итак, в искомую сумму войдет 225 слагаемых. Найдем сумму 225 членов арифметической прогрессии с первым членом 103 и разностью 4:

Пример 4

Известно, что при любом n сумма Sn членов в некоторой последовательности (an) определяется по формуле Докажите, что эта последовательность является арифметической прогрессией, и напишите первые три члена этой прогрессии.

Для доказательства используем определение арифметической прогрессии. Сначала получим формулу общего члена последовательности (аn). Очевидно, что Отсюда:

Рассмотрим разность двух соседних членов последовательности: Отсюда получим: аn = аn-1 + 8, т. е. каждый член последовательности равен предыдущему, сложенному с одним и тем же числом 8. Итак, данная последовательность по определению является арифметической прогрессией.

Так как в процессе доказательства была получена формула общего члена этой арифметической прогрессии аn = 8n - 7, то легко находим: a1 = 1, а2 = 9, а3 = 17.

Пример 5

Решить уравнение 2 + 5 + 8 + 11 + ... + х = 155.

В левой части уравнения находится сумма членов арифметической прогрессии: 2; 5; 8; 11; ..., первый член которой 2 и разность 3. Пусть в эту сумму входит n слагаемых. Тогда, используя формулу для суммы n первых членов арифметической прогрессии, получаем: Второе уравнение получим, записав последний член этой суммы: х = 2 + 3(n - 1) = 3n - 1. Подставив второе уравнение в первое, придем к квадратному уравнению относительно n: или 3n2 + n - 310 = 0, корни которого n = 10 и n = -31/3 (не подходит, т. к. n - число натуральное).

После этого находим: х = 3 · 10 - 1 = 29. Итак, х = 29 — единственный корень данного уравнения.

Пример 6

Два велосипедиста, расстояние между которыми 99 м, одновременно начинают движение навстречу друг другу. Первый велосипедист за каждую секунду проезжал по 5 м. Второй велосипедист за первую секунду проехал 1,5 м, а за каждую последующую – на 0,5 м больше, чем за предыдущую. Через какое время велосипедисты встретились?

Пусть велосипедисты встретились через n сек. Тогда первый из них проехал до встречи 5n (м). Для второго велосипедиста расстояния, проезжаемые в каждую секунду, образуют арифметическую прогрессию: 1,5; 2; 2,5; 3; ... Тогда за n сек он проедет расстояние:

Сума расстояний, пройденных велосипедистами, равна 99 м. Получаем уравнение или n2 + 25n - 396 = о, корни которого n1 = 11 и n2 = -36 (не подходит). Итак, встреча произошла через 11 сек.

IV. Задание на уроке

№ 603 (а); 604 (б); 606 (а); 608 (б); 609 (а, в); 610; 612; 615 (а); 617.

V. Задание на дом

№ 603 (б); 604 (а); 606 (б); 608 (а); 609 (б, г); 611; 613; 615 (б); 618.

VI. Подведение итогов урока

§ 10. Геометрическая прогрессия