Вероятность равновозможных событий - Начальные сведения из теории вероятностей - Элементы комбинаторики и теории вероятностей

Цель: рассмотреть понятие вероятности события.

Ход урока

I. Сообщение темы и цели урока

II. Изучение нового материала

Разумеется, проведение реальных испытаний для нахождения вероятности событий очень трудоемко. Например, было проведено 80 640 подбрасываний монеты и экспериментально определена вероятность 0,4923 выпадения орла. Если на одно подбрасывание тратить только одну секунду, то на такие опыты потребуется более суток. Поэтому необходимо определять вероятность события путем рассуждений. Обсудим этот способ.

Подбрасывая монету, мы понимаем, что шансы выпадения орла и решки одинаковы. Тогда вероятность выпадения орла равна 1/2.

Точно гак же одинаковы шансы выпадения любой из граней на игральной кости. Вероятность такого выпадения равна 1/6. В подобных случаях считают, что события равновозможны.

Пусть нас интересует результат бросания кубика, при котором число очков кратно 3 (т. е. три очка или шесть очков). Исходы бросаний, при которых появляется интересующий нас результат, называют благоприятными.

Вероятностью Р появления некоторого события называют отношение числа т случаев, благоприятствующих появлению этого события, к общему числу п равновозможных в данном опыте случаев, т. е. Р = m/n .

Приведем примеры вычисления вероятностей.

Пример 1

В мешке 18 шаров: 5 белых, 3 зеленых и 10 красных. Найдем вероятность того, что вытащенный наугад шар будет заданного цвета.

Мы можем вытащить любой из 18 шаров, т. е. n = 18.

Благоприятные исходы: появление белого шара (mб = 5), зеленого шара (mз = 3), красного шара (mк = 10).

Находим вероятность появления белого шара: зеленого шара: красного шара:

Пример 2

Найдем вероятность того, что при подбрасывании двух костей суммарное число очков окажется равным 5.

Возможно следующее сочетание очков на первой и второй костях: 1 + 4, 2 + 3, 3 + 2, 4 + 1 - четыре благоприятных случая (m = 4).

Всего возможных исходов: n = 6 · 6 = 36 (по шесть для каждой кости).

Тогда вероятность рассматриваемого события равна:

Пример 3

Из класса, в котором 15 девочек и 10 мальчиков, жеребьевкой выбирают команду численностью 15 человек для игры в КВН. Какова вероятность того, что будут выбраны 10 девочек и 5 мальчиков?

Из 25 человек команду численностью 15 человек можно выбрать n = С2515 способами.

Выбрать 10 девочек из 15 можно С1510 способами, выбрать 5 мальчиков из 10 можно С105 способами.

Всего скомплектовать команду можно способами. Поэтому вероятность рассматриваемого события

Видно, что вероятность такого события чрезвычайно мала - один шанс из четырех миллионов.

Событие, которое происходит всегда, называют достоверным событием. Например, событие, состоящее в том, что при бросании игральной кости выпадет натуральное число очков. Вероятность достоверного события равна 1.

Событие, которое не может произойти, называют невозможным. Например, выпадение 9 очков на игральной кости. Вероятность невозможного события равна 0.

Таким образом, вероятность Р некоторого события 0 ≤ Р ≤ 1. Заметим, что понятие вероятности позволяет решать практические задачи.

Пример 4

Как приближенно посчитать число рыб в озере?

Пусть в озере плавает х рыб. Бросаем сеть и отлавливаем n рыб. Вероятность поймать одну рыбу Р = n/x. Пометим этих рыб и выпустим в озеро. Через несколько дней в ту же погоду, в том же месте ставим ту же сеть. Предположим, что поймали m рыб, из них k - меченых х. Меченая рыба поймалась с вероятностью Р = k/m. Получаем равенство откуда

Разумеется, точность такого эксперимента будет невысокой, но для оценки числа рыб в озере вполне допустима.

Вероятность случайного события иногда можно найти, используя геометрические соображения.

Предположим, что точку бросают в фигуру площади S. Пусть эта фигура содержит фигуру площади а. Будем считать вероятностью Р попадания точки в меньшую фигуру отношение a/S, т. е. Р = a/S.

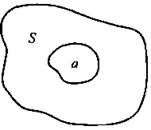
Пример 5

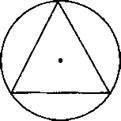
В окружность вписан правильный треугольник. Найдем вероятность того, что точка, брошенная в круг, попадет в треугольник.

Пусть радиус окружности равен R, а сторона треугольника равна с. Свяжем между собой эти переменные. Используем теорему синусов: откуда

Найдем вероятность попадания точки в треугольник:

Пример 6

Коля и Миша договорились встретиться в условленном месте с 10 ч до 10 ч 30 мин, причем каждый пришедший ждет другого 10 мин, после чего уходит. Найдите вероятность того, что встреча состоится, если каждый выбирает момент своего прихода наудачу в указанном интервале.

Пусть х - момент прихода на место встречи Коли, у - момент прихода Миши. Так как время ожидания составляет 10 мин, то для встречи необходимо выполнение неравенства |у - х| ≤ 10, или -10 ≤ у – х ≤ 10, или x – 10 ≤ у ≤ х + 10.

На координатной плоскости построим квадрат со стороной 30. Каждая точка этого квадрата соответствует времени прихода мальчиков. Построим также множество точек, удовлетворяющих неравенству x – 10 ≤ у ≤ х + 10 (эта область заштрихована). Тогда вероятность встречи мальчиков равна отношению площади заштрихованной фигуры к площади квадрата.

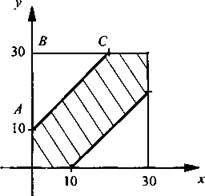
Площадь квадрата равна 302 = 900. Найдем площадь треугольника АВС и получим:

Тогда площадь заштрихованной фигуры: 900 – 2 · 200 = 500.

Вероятность встречи мальчиков 500/900 = 5/9.

III. Контрольные вопросы

1. Равновозможные события.

2. Благоприятные исходы события.

3. Понятие вероятности события.

4. Достоверное событие и невозможное событие.

5. Понятие геометрической вероятности.

IV. Задание на уроке

№ 799; 801; 803; 805; 807; 809; 811; 814.

V. Задание на дом

№ 798; 800; 802; 804; 808; 810; 812; 815; 816.

VI. Подведение итогов урока