Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003

Задачи
Делимость многочленов. Теорема Безу. Целые уравнения

Многочлен S(x) называется частным, а многочлен R(x) — остатком от деления многочлена P(x) на многочлен Q(x), если равенство

P(x) = Q(x) · S(x) + R(x)

является тождеством и степень многочлена R(x) меньше степени многочлена Q(x).

Обобщенная теорема Виета. Для корней х₁, х₂, ..., х_n уравнения

а₀хⁿ + a₁x^{n − 1} + ... + а_{n − 1}x + а_n = 0

имеют место формулы:

^,

^,

.

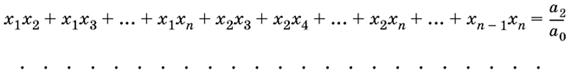
Для уравнения a₀xⁿ + a₁x^{n − 1} + ... + а_n = 0 с целыми коэффициентами а₀, а₁, ... , а_n верна теорема: если уравнение имеет рациональный корень ^p/_q , то p числитель является делителем свободного члена а_n, а знаменатель q — делителем коэффициента а₀.

В частности, если а₀ = 1, то уравнение может иметь только такие целые корни, которые являются делителями свободного члена а_n.

8.1. Решите уравнение

(x − 4,5)⁴ + (x − 5,5)⁴ = 1.

8.2. Решите уравнение

(4x + 1)(12x − 1)(3x + 2)(x + 1) = 4.

8.3. Докажите, что уравнение

x² − 3у² = 17

не имеет решений в целых числах.

8.4. Найдите все целые решения уравнения

x² − 6xу + 13у² = 100.

8.5. Найдите остаток от деления многочлена x⁹⁹ + x³ + 10x + 5 на многочлен x² + 1.

8.6. Найдите все целочисленные решения уравнения

2x²у² + у² − 6x² − 12 = 0.

8.7. В уравнении

x⁴ + аx³ + bx² + 6x + 2 = 0

один из корней равен √3 + 1. Найдите остальные корни уравнения, если а и b — рациональные числа.

8.8. При каких значениях а оба корня уравнения

x² − (а + 1)x + а + 4 = 0

отрицательны?

8.9. Найдите соотношение между а, b и с, если корни уравнения

x³ + аx² + bx + с = 0

образуют геометрическую прогрессию.

8.10. Известно, что уравнение x³ + px + q = 0 имеет корни α₁, α₂, α₃. Выразите сумму α₁² + α₂² + α₃² через p и q.

8.11. При каких а и α трехчлен х³ + ax + 1 делится на двучлен x − α без остатка и частное от деления при всех x больше нуля?

8.12. Остатки от деления многочлена относительно x на x − 2 и x − 3 равны соответственно 5 и 7. Найдите остаток от деления этого многочлена на (x − 2)(x − 3).

8.13. Найдите все действительные значения p и q, при которых х⁴ + 1 делится на x² + рх + q.

8.14. Докажите, что многочлен

x²^{n + 1} − (2n + 1)х^{n + 1} + (2n + 1)хⁿ − 1,

где n — натуральное число, делится на (x − 1)³.

8.15. Определите p и q так, чтобы многочлен

6х⁴ − 7х³ + рх² + 3х + 2

делился без остатка на x² − x + q.