Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Задачи
Тригонометрические уравнения и системы
Простейшие тригонометрические уравнения.
sin x = а, x = nπ + (−1)n arcsin а, |а| ≤ 1,
cos x = а, x = 2nπ ± arccos а, |а| ≤ 1,
tg x = а, x = nπ + arctg а,
ctg x = а, x = nπ + arcctg а.
Во всех формулах n — произвольное целое число, т. е. n = 0; ±1; ±2; ±3; ... .
Решения уравнения sin x = а часто удобно записывать в виде двух серий корней:
x = 2nπ + αrсsin а, x = π(2n + 1) − arcsin а.
Хотя приведенные формулы для решений уравнений sin x = а и cos x = а верны при всех значениях а, удовлетворяющих указанным справа ограничениям, при некоторых а эти формулы дают неудобный ответ.
Так, например, если к уравнению sin x = 1 применить общую формулу, то получим
x = nπ + (−1)n π/2.
При n = 2k получим x = 2kπ + π/2, а при n = 2k + 1 получим x = 2kπ + π − π/2 = 2kπ + π/2. При четном и нечетном n мы пришли к одинаковому ответу. Но этот же ответ можно получить гораздо проще, если не пользоваться общей формулой. Достаточно заметить, что sin x = 1 тогда и только тогда, когда подвижный радиус вертикален и направлен вверх.
Поэтому целесообразно помнить решения уравнений:
sin x = 0, x = nπ; sin x = 1, x = π/2 + 2nπ; sin x = −1, x = − π/2 + 2nπ;
cos x = 0, x = π/2 + nπ; cos x = 1, x = 2nπ; cos x = −1, x = (2n + 1)π;
tg x = 0, x = nπ; ctg x = 0, x = π/2 + nπ.
При решении уравнений удобно пользоваться теоремами: уравнение cos x = cos у равносильно совокупности уравнений x + у = 2kπ, x − у = 2lπ; уравнение sin x = sin у равносильно совокупности уравнений x + у = (2k + 1)π, x − у = 2lπ. Обратите внимание на то обстоятельство, что в разных уравнениях, входящих в совокупность, вообще говоря, используют разные буквы для обозначения произвольного целого числа. Это следует из того, что уравнения для x + у и для x − у решаются независимо одно от другого. Переход от уравнения tg x = tg у к уравнению x − у = πk может привести к приобретению посторонних решений, если tg x и tg у перестают существовать.
Однородные уравнения. Уравнение вида
а0 sink x + а1 sink − 1 x cos x + ...
... + аk − 1 sin x cosk − 1 x + аk cosk x = 0 (1)
называется однородным, так как все слагаемые его левой части имеют одинаковую степень относительно sin x и cos x.
При α0 ≠ 0 среди решений уравнения (1) не содержится значений x, при которых cos x = 0. В самом деле, полагая cos x = 0, мы получаем из уравнения (1): а0 sink x = 0, откуда sink x = 0, так как а0 ≠ 0 по условию. Но это невозможно, поскольку нет таких значений x, при которых sin x и cos x одновременно обращаются в нуль.
Аналогично при ак ≠ 0 среди решений уравнения (1) не содержится значений x, при которых sin x = 0.
Наметим пути решения уравнения (1). Рассмотрим два случая.
Случай 1. a0 ≠ 0 и аk ≠ 0. В этом случае, разделив уравнение (1) на cosk x, мы получим (поскольку cos x ≠ 0) равносильное ему алгебраическое уравнение
а0ук + а1уk − 1 + ... + аk − 1у + аk = 0 (2)
относительно у = tg x.
Можно также делить уравнение (1) на sink x. Тогда (поскольку sin x ≠ 0) мы получим равносильное уравнению (1) алгебраическое уравнение
а0 + а1z + ... + аk − 1zk − 1 + аkzk = 0 (3)
относительно z = ctg x.
Пример 1. Решить уравнение
sin³ x − 2 sin² x cos x − sin x cos² x + 2 cos³ x = 0. (4)
Разделив его на cos³ x, получим алгебраическое уравнение
у³ − 2у² − у + 2 = 0,
где у = tg x. Последнее уравнение легко решается путем разложения его левой части на множители, и мы находим корни:
у1 = −1, у2 = 1, у3 = 2.
Теперь остается решить совокупность уравнений
tg x = −1, tg x = 1, tg x = 2.
Мы получим следующие корни уравнения (1):
x = nπ ± π/4 , x = nπ + arctg 2.
Случай 2. a0 = 0, или ak = 0, или а0 = ak = 0. Пусть, например, a0 = ak = 0, а a1 ≠ 0 и ak − 1 ≠ 0. Тогда уравнение (1) примет вид
a1 sink − 1 x cos x + a2 sink − 2 x cos² x + ...
... + ak − 2 sin² x cosk − 2 x + ak − 1 sin x cosk − 1 x = 0. (5)
В левой части уравнения выносим за скобки все, что возможно (в случае уравнения (5) мы можем вынести за скобки произведение sin x cos x). В результате получим уравнение
sin x cos x (a1 sink − 1 x + a2 sink − 2 x cos x + ...
... + ak − 2 sin x cosk − 2 x + ak − 1 cosk − 1 x) = 0,
распадающееся на совокупность уравнений
sin 2х = 0,
a1 sink − 1 x + a2 sink − 2 x cos x + ...
... + ak − 2 sin x cosk − 2 x + ak − 1 cosk − 1 x = 0,
первое из которых решается просто (см. с. 77), а пути решения второго уравнения показаны в случае 1).
Пример 2. Решить уравнение
sin4 x cos x − 2 sin³ x cos² x − sin² x cos³ x + 2 sin x cos4 x = 0.
Левую часть уравнения разлагаем на множители:
sin x cos x (sin³ x − 2 sin² x cos x − sin x cos² x + 2 cos³ x) = 0. Получаем совокупность уравнений
sin x = 0, cos x = 0,
sin³ x − 2 sin² x cos x − sin x cos² x + 2 cos³ x = 0.
Решения первых двух уравнений даны на с. 77. Третье уравнение подробно рассмотрено в примере 1.
Системы тригонометрических уравнений. Предположим, что, преобразовывая систему тригонометрических уравнений, мы пришли к системе
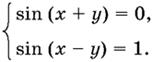
Если переписать эту систему в виде
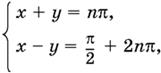
то, складывая и вычитая полученные уравнения, придем к выводу, что
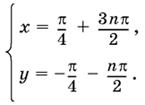
Решили ли мы систему? Оказывается, нет. Решить систему — значит, найти все ее решения, а из поля нашего зрения выпало такое очевидное решение как x = 3π/2, у = π/4 (ни при каком целом n из выражения π/4 + 3nπ/2 нельзя получить 3π/4).
В чем же ошибка? Ошибка очень проста: переходя от первоначальной системы к выражениям относительно x + у и x − у, мы должны были сохранить их «независимость», которая присутствовала в исходной системе. Вместо этого мы «связали» их введением общего целочисленного переменного n.
Правильным было бы такое решение:
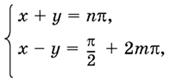
откуда
x = π/4 + (2т + n), у = − π/4 − π/2 (2т − n).
Прежде чем приступать к решению задач, ознакомьтесь с введением к главе 9.
Решите уравнения:
13.1. 1 + sin 2x + 2√2 cos 3x sin (x + π/4) = 2 sin x + 2 cos 3x + cos 2x.
13.2.
![]()
.
13.3.
![]()
.
13.4. tg 2x tg 7x = 1.
13.5.
![]()
13.6. 2 tg 3x − 3 tg 2x = tg² 2x tg 3x.
13.7. sin³ x + cos³ x + 1/√2 sin 2x sin (x + π/4) = cos x + sin 3x.
13.8. 4 tg 4x − 4 tg 3x − tg 2x = tg 2x tg 3x tg 4x.
13.9. Найдите решения уравнения
![]()
лежащие в интервале (0, 2π).
13.10. Решите уравнение
sin (x − α) = sin x − sin α.
13.11. Найдите решения уравнения
|cos 2x| = |sin² x − а|
(а — действительное число), удовлетворяющие неравенству
0 ≤ x ≤ 2π.
Решите уравнения:
13.12.
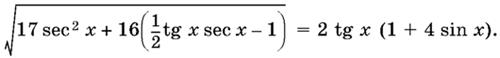
13.13. (tg x + sin x)½ + (tg x − sin x)½ = 2 tg½ x cos x.
13.14. ctg 2x + 3 tg 3x = 2 tg x + 2/sin 4x.
13.15. sec x² + cosec x² + sec x² cosec x² = 1.
13.16.
![]()
13.17. 4 sin x + 2 cos x = 2 + 3 tg x.
13.18. cos x = cos² 3x/4.
13.19. sin 4x[2 + ctg x + ctg (π/4 − x) = 2√2(1 + sin 2x + cos 2x).
13.20. sin 4x sin x − sin 3x sin 2x = ½ cos 3x + (1 + cos x)½ .
13.21. sin 4x = m tg x, где m > 0.
13.22. sin x/2 (sin x + sin 2x + ... + sin 100x) = ½ sin 101x/2.
13.23. sin² x + sin 2x sin 4x + ... + sin nx sin n²x = 1.
13.24. 4 cos x − 2 cos 2x − cos 4x = 1.
13.25.
![]()
13.26. sin³ x + cos³ x = 1.
13.27. cos² 3x + ¼ cos² x = cos 3x cos4 x.
13.28. При каких значениях а уравнение
1 + sin² ax = cos x
имеет единственное решение?
Решите системы:
13.29.
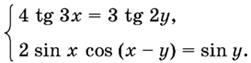
13.30.
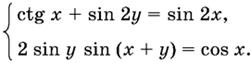
13.31.
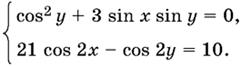
13.32.
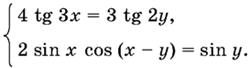
13.33.
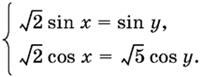
13.34.
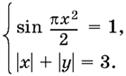
13.35.
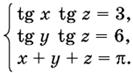
13.36.
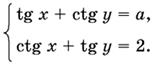
13.37.
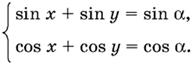
13.38.
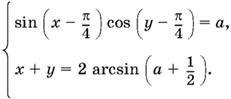
13.39. Найдите все пары чисел x, у, которые удовлетворяют уравнению
tg4 x + tg4 у + 2 ctg² x ctg² у = 3 + sin² (x + у).
13.40. Решите уравнение
sin² x + ¼ sin² 3x = sin x sin² 3x.
13.41. Решите уравнение
cos x + cos у − cos (x + у) = 3/2.
13.42. Найдите все пары чисел а и b, при которых для любых x и у, удовлетворяющих условию x + у = а (где x ≠ π/2 + nπ, у ≠ π/2 + nπ, n, m = 0, ±1, ±2, ...), верно равенство tg x + tg у + tg x tg у = b.
13.43. Найдите все пары чисел x и у, которые удовлетворяют уравнению
![]()
13.44. Решите уравнение
sin x + 2 sin 2x = 3 + sin 3x.
13.45. Решите уравнение
sin x (cos x/4 − 2 sin x) + cos x (1 + sin x/4 − 2 cos x) = 0
13.46. Решите уравнение
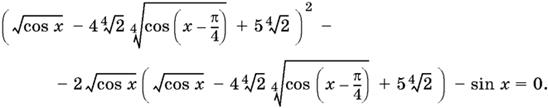
13.47. Найдите все значения x, удовлетворяющие одновременно следующим уравнениям:
cos 6х + cos 8х = 0, cos Зх = 2 sin² 2х
при условии, что |x| < 5.
13.48. Решите уравнение
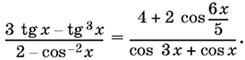
13.49. Решите уравнение
![]()
13.50. Решите уравнение
2 tg x + tg x/2 + 4 ctg 2х = ctg Зх.
13.51. Решите уравнение
![]()