Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Решения
Геометрические места
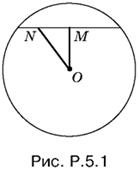
5.1. Из любой точки M (рис. P.5.1) отрезок ON виден под прямым углом. Следовательно, искомое геометрическое место точек — окружность, построенная на отрезке ON, как на диаметре.
5.2. Пусть точка M принадлежит искомому геометрическому месту точек. По теореме косинусов для треугольника AMB (рис. P.5.2) имеем
AB² = AM² + BM² − 2AM · BM cos α.
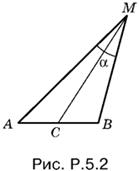
Так как AM · BM cos α = ¾AB², то
AM² + BM² = 5/2AB². (1)
Если МС — медиана треугольника АМВ, то
4MC² = 2АМ² + 2ВМ² − АВ².
Воспользуемся соотношением (1) и заменим 2(АМ² + ВМ²) на 5АВ²:
4МС² = 5АВ² − АВ², т. е. МС = AB.
Итак, искомое геометрическое место точек — окружность радиусом AB с центром в середине AB.
5.3. Докажем вначале, что если точка M лежит на рассматриваемой окружности, то выполняется сформулированное в условии задачи соотношение. Обозначим центр окружности буквой O и выберем на окружности произвольную точку M, отличную от А и С (рис. P.5.3).
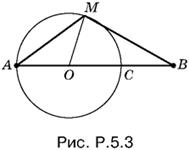
Применим к стороне МВ треугольника АМВ теорему косинусов:
МВ² = АМ² + АВ² − 2АМ · AB cos А.
Из треугольника АMO находим AM = 2АO cos А, откуда cos А = AM/2AO. По условию АO = AB/3. Подставляя cos А = 3/2AM/AB в выражение для МВ², получим МВ² = АМ² + АВ² − ЗАМ², т. е. 2АМ² + МВ² = АВ², что и требовалось проверить.
Простой проверкой легко убедиться, что это соотношение справедливо, если M совпадает с А и если M совпадает с С. B первом случае AM = 0, а МВ = AB и равенство становится очевидным AB² = АВ². Во втором случае AM = AC = ⅔AB, МВ = СВ = ⅓AB и
2(⅔AB)² + (⅓АВ)² = АВ².
Перейдем к доказательству обратного утверждения.
Докажем, что если в треугольнике АМВ
3АO = AB и 2АМ² + МВ² = АВ²,
то АO = MO, т. е. точка M лежит на окружности радиусом АO. Начнем со случая, когда M не лежит на AB. Предыдущие рассуждения подсказывают нам, что полезно воспользоваться не только данным соотношением, но и теоремой косинусов для треугольника АМВ:
МВ² = АМ² + АВ² − 2АМ · AB cos А.
Так как мы не знаем, чему равен cos А, то постараемся его исключить. Запишем теорему косинусов для стороны MO треугольника АMO (учтем при этом, что 3АO = AB):
MO² = АМ² + 1/9АВ² − ⅔AM · AB cos А.
Умножив последнее равенство на −3 и сложив с выражением для МВ², получим
МВ² − 3MO² = −2АМ² + ⅔АВ².
Заменяя МВ² + 2АМ² на АВ², придем к равенству
АВ² = 3MO² + 3/2АВ², т. е. АВ² = 9MO²,
откуда AB = 3MO и MO = АO, что и требовалось показать.
Если теперь точка M лежит на прямой AB, то она может располагаться либо на отрезке AB (включая его концы), либо вне этого отрезка.
Пусть точка M расположена вне отрезка AB. Тогда или AM + AB = МВ, или МВ + AB = AM. B первом случае получаем AB = МВ − AM, а после возведения в квадрат: АВ² = АМ² + МВ² − 2АМ · МВ. Заменяя АВ² на 2АМ² + МВ², придем к равенству AM = −2МВ, которое абсурдно. Аналогично рассматривается второй случай.
Пусть теперь точка M расположена на отрезке AB. Тогда AM + МВ = AB, что после возведения в квадрат и замены АВ² на 2АM² + МВ² приводит к равенству
АМ² = 2МВ · AM.
Из этого равенства следует, что либо AM = 0 (точки А и M совпадают), либо AM = 2МВ (точка M совпадает с точкой С).
Тем самым доказательство полностью завершено.
5.4. B треугольниках АВМ и ВМС при любом их расположении сторона ВМ общая. Если выбрать ее в качестве основания, то для равенства площадей этих треугольников необходимо и достаточно равенство высот, т. е. площади треугольников равны тогда и только тогда, когда прямая ВМ отстоит от точек А и С на одинаковое расстояние. Так как точки А и С зафиксированы, то задача состоит в нахождении всех прямых равноудаленных от А и С.
Если прямая ВМ пересекает отрезок AC (рис. P.5.4, а), то из равенства высот h1 и h2 следует, что треугольники АВF и CВF равновелики. Поскольку они имеют общую высоту, соответствующую вершине B, их основания АF и CF равны, и прямая, равноотстоящая от А и С, проходит в этом случае через середину отрезка AC.
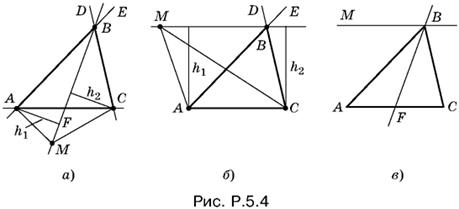
Если же прямая ВМ не пересекает отрезок AC (рис. P.5.4, б), то из равенства высот h1 и h2 следует, что ВМ || AC.
Остается убедиться, что любая точка прямых ВМ, изображенных на рис. P.5.4, а и P. 5.4, б, удовлетворяет условию задачи. Следовательно, прямые ВМ и BF (рис. P.5.4, в) образуют искомое геометрическое место точек.
5.5. Рассмотрим вначале случай, когда прямые AB и CD, на которых лежат данные отрезки, пересекаются в некоторой точке N (рис. P.5.5, а). Пусть точка M принадлежит искомому геометрическому месту. Площади треугольников АВМ и CDM не изменятся, если каждый из отрезков AB и CD двигать по несущей его прямой. Переместим отрезки так, чтобы они имели своим общим концом точку N. Отрезок AB перейдет в NB′, а отрезок CD — в ND′. Поскольку пары треугольников АВМ, NB′M и CDM, ND′M равновелики, то искомое геометрическое место точек можно характеризовать тем свойством, что площади треугольников NB′M и ND′M равны.
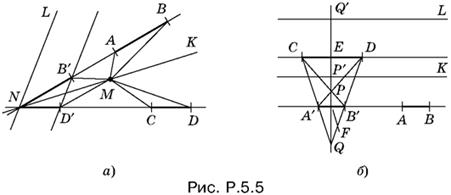
Итак, задача свелась к предыдущей (см. задачу 5.4): для треугольника B′ND′ найти геометрическое место точек M таких, что площади треугольников NB′M и ND′M равны. Мы уже доказали, что это — две прямые NK и NL, первая из которых проходит через середину B′D′, а вторая параллельна B′D′.
Рассмотрим теперь случай, когда прямые AB и CD параллельны. Сместим отрезок AB по несущей его прямой так, чтобы его центр совпал с центром CD (рис. P.5.5, б). Если точка M (на рисунке она не изображена) принадлежит искомому геометрическому месту точек, то отношение ее расстояния до прямых AB и CD есть отношение высот в треугольниках АВМ и CDM. Площади этих треугольников будут равны тогда и только тогда, когда отношение расстояний от точки M до AB и CD будет равно отношению отрезков CD и AB. Таким образом, искомое геометрическое место есть две параллельные прямые, расстояния которых до CD и AB относятся как AB : CD.
Чтобы построить это геометрическое место точек, сместим отрезок AB по несущей его прямой так, чтобы его центр и центр E отрезка CD оказались на общем перпендикуляре к AB и CD (см. рис. P.5.5, б). Прямые DA′ и CB′ пересекутся в точке P, которая делит EF в отношении PF : РЕ = AB : CD, а прямые DB′ и СА′ пересекутся в точке Q, для которой QF : QE = AB : CD. Остается на прямой EF (см. рис. P.5.5, б) построить отрезки EP′ = FP и EQ′ = FQ. Прямые P′K и Q′L, проведенные через P′ и Q′ параллельно AB и CD, образуют искомое геометрическое место точек.
5.6. Для данного куба с ребром а найдем сначала геометрическое место середин отрезков длины l, один из концов которых лежит на диагональной прямой верхнего основания, а другой — на не параллельной ей диагональной прямой нижнего основания. Как мы увидим, замена диагоналей на диагональные прямые позволяет упростить задачу.
Если MN — отрезок длины l, о котором идет речь в условии задачи, а расстояние между плоскостями верхнего и нижнего оснований равно а, то проекция MK отрезка MN на плоскость нижнего основания равна
![]()
(рис. P.5.6, а). Проекция G середины E отрезка MN делит MK пополам, поэтому
![]()
Треугольник MKO прямоугольный, а GO — его медиана. Следовательно,
![]()
Тем самым мы установили, что для фиксированного l точка G всегда отстоит от точки О на одинаковом расстоянии, равном
![]()
, т. е. лежит на окружности радиусом
![]()
с центром в точке О.
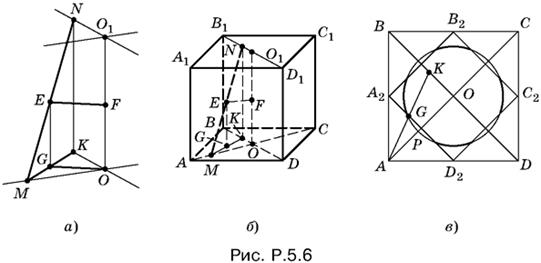
Итак, если точка E принадлежит искомому геометрическому месту, то она лежит в плоскости, параллельной основаниям куба и проходящей через середину F отрезка OO1, и принадлежит окружности радиусом
![]()
с центром в точке F.
Для той измененной задачи, которую мы рассматриваем, верно и обратное утверждение: любую точку E, принадлежащую описанной выше окружности, можно спроецировать в точку G плоскости нижнего основания и радиусом GO сделать из точки G засечки M и K на диагональных прямых нижнего основания. Построив перпендикуляр NK, мы сможем найти и отрезок МN длины l, серединой которого является точка E.
Теперь остается учесть тот факт, что точка E и отрезок МN не должны покидать пределы куба.
Для этого нужно уловить тот момент, после которого один конец отрезка MN, например M, покинет куб. Ясно, что это произойдет, когда точка M совместится с одной из вершин квадрата ABCD. Пусть точка M совпала с вершиной А (рис. P.5.6, б). B зависимости от длины l отрезка МN проекция K точки N расположится на отрезке OB. При изменении длины отрезка МN точка K пробегает весь отрезок BO, а середина G отрезка MK пробегает в это время отрезок А2Р, являющийся средней линией треугольника АВO.
Теперь ясно, что проекция точки E на плоскость нижнего основания куба не может выйти из квадрата А2В2С2D2 (рис. P.5.6, в).
Итак, искомое геометрическое место точек расположено в горизонтальном сечении куба, проходящем через его центр. Это — часть окружности с центром в центре куба, не выходящая за пределы квадрата, проецирующегося в А2В2С2D2.