Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Решения
Тригонометрические неравенства
14.1. Неравенство равносильно такому:
sin² x > cos² x,
т. е.
cos² x − sin² x < 0, cos 2x < 0,
откуда
π/2 + 2nπ < 2x < 3π/2 + 2nπ.
Ответ. π/4 + nπ < x < 3π/4 + nπ.
14.2. Перепишем неравенство в виде
1/√2 cos x − 1/√2 sin x < −1/√2,
откуда
cos (x + π/4) < −1/√2,
т. е.
3π/4 + 2nπ < x + π/4 < 5π/4 + 2nπ
Ответ. π/2 + 2nπ < x < π + 2nπ.
14.3. Способ 1. Неравенство sin x < 3 cos x равносильно совокупности трех систем
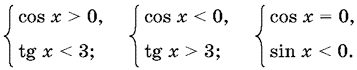
Решение каждой из них изображено на рис. P. 14.3.
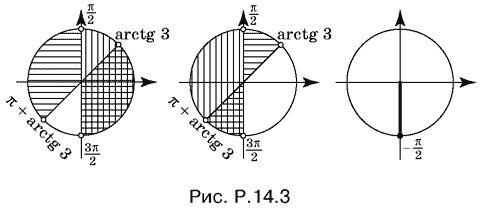
Способ 2. Запишем данное неравенство так:
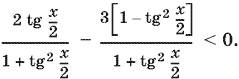
При использовании этих формул мы исключили из области существования левой части неравенства точки, в которых tg x/2 не существует. Поэтому нужно подставить в исходное неравенство x = π(2n + 1). Убеждаемся, что
sin π(2n + 1) − 3 cos π(2n + 1) = 3,
т. е. эти точки не являются корнями неравенства.
Приходим к квадратному неравенству
3 tg² x/2 + 2 tg x/2 − 3 < 0,
откуда
![]()
Наиболее компактный ответ получается при решении неравенства первым способом.
Ответ. arctg 3 + π(2n + 1) < x < arctg 3 + 2πn.
14.4. Поскольку tg x входит в правую часть данного неравенства, замена sin 2x и cos 2x их выражениями через tg x приведет к равносильному неравенству. Обозначив tg x = y, получим
![]()
Так как 1 + y² > 0, то это неравенство равносильно такому:
y³ + 2y² − y − 2 < 0.
Сгруппировав первый член с третьим, а второй с четвертым, разложим левую часть на множители:
(y + 2)(y + 1)(y − 1) < 0.
Решения этого неравенства будут лежать в интервалах
y < −2, −1 < y < 1,
т. е.
tg x < − 2, −1 < tg x < 1.
Ответ. −π/2 + nπ < x < −arctg 2 + nπ; −π/4 + nπ < x < π/4 + nπ.
14.5. Способ 1. Неравенство равносильно совокупности двух систем
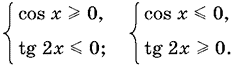
Начнем со второго неравенства. При решении обеих систем нам понадобятся радиусы, на которых tg 2x = 0 и tg 2x не существует, так как только в этих точках может произойти перемена знака.
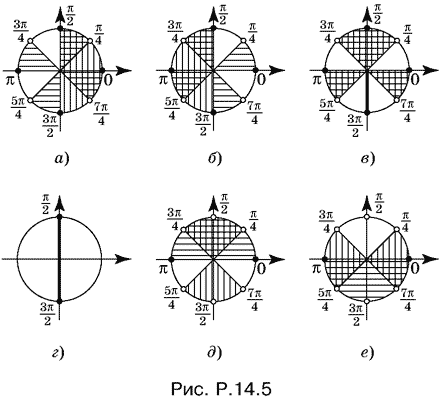
Эти радиусы нанесены на рис. P.14.5, а и б, причем на первом горизонтальной штриховкой заштрихованы те секторы, где tg 2x < 0, а на втором — остальные секторы круга. Остается в первом случае выбрать секторы, в которых cos x ≥ 0, а во втором — в которых cos x ≤ 0.
Нанесем решения данного неравенства на общий чертеж (рис. P.14.5, в), после чего можно записать ответ.
Способ 2. Воспользуемся формулой тангенса двойного угла и перепишем неравенство в виде
![]()
Формула, которую мы применили, является неабсолютным тождеством, так как в результате ее использования из области определения левой части неравенства исчезают значения x, при которых cos x = 0. Непосредственной подстановкой в исходное неравенство убеждаемся, что x = π/2 + kπ — его корни. Отметив соответствующие радиусы на чертеже (рис. P.14.5, г), можем считать, что cos x ≠ 0, и решать неравенство
![]()
Когда sin x ≥ 0, то получим tg x < −1, tg x > 1 (рис. P.14.5, д), а когда sin x ≤ 0, то −1 < tg x < 1 (рис. P.14.5, e). Объединяя все решения на одном чертеже (не забывайте про рис. P.14,5, г), запишем окончательный ответ (см. рис. P.14.5, в).
Ответ. π/4 + 2nπ < x < 3π/4 + 2nπ; π + 2nπ ≤ x < 5π/4 + 2nπ; 7π/4 + 2nπ < x ≤ 2(n + 1)π; x = (4n − 1)π/2.
14.6. Выразим все тригонометрические функции через cos x = y. Получим неравенство
2y² + 13y + 5 ≥ |2y² − 3y + 1|.
Оно равносильно совокупности систем
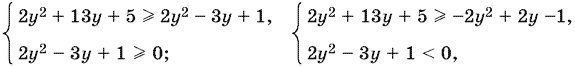
или
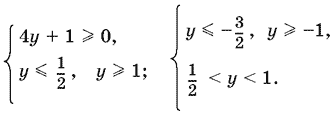
Так как y = cos x, то −1 ≤ y ≤ 1. Учитывая это ограничение, получим
−¼ ≤ y ≤ ½, y = 1, ½ < y < 1,
т. е.
cos x ≥ −¼.
Ответ. π(2k − 1) + arccos ¼ ≤ x ≤ π(2k + 1) − arccos ¼.
14.7. Если cos x = 0, то sin² x = 1 и неравенство не удовлетворяется.
Поделим обе части неравенства на cos² x и обозначим tg x = y. Получим алгебраическое неравенство
√2 y² − 2y + 2 − √2 < 0.
Разделив на √2, получим неравенство
y² − √2 y + √2 − 1 < 0,
откуда
√2 − 1 < tg x < 1.
Из интервалов, в которых лежит x:
arctg (√2 − 1) + nπ < x < π/4 + nπ,
выбираем решения, лежащие в (0, 2π).
Ответ. arctg (√2 − 1) < x < π/4; π + acrtg (√2 − 1) < x < 5π/4.
14.8. Дискриминант трехчлена равен
(2 cos α − 1)² − 4 cos² α + 10 cos α − 4 = 6 cos α − 3.
Чтобы уравнение имело различные действительные корни, нужно потребовать
6 cos α − 3 > 0; т. е. cos α > ½,
откуда 0 ≤ α < π/3 (в условии сказано, что 0 ≤ α ≤ π).
Свободный член сравним с нулем:
2cos² α − 5cos α + 2 ∨ 0.
Так как корнями трехчлена 2y² − 5у + 2 будут числа ½ и 2, то свободный член будет положителен при cos α < ½ и отрицателен при cos α > ¼. Мы уже выяснили, что должно иметь место второе неравенство; таким образом, исходное уравнение имеет корни разных знаков.
Поскольку x1 + x2 = 2cos α − 1, что при cos α > ½ больше нуля, то положительный корень имеет большую абсолютную величину.
Ответ. Данное уравнение имеет два различных действительных корня при 0 ≤ α < π/3. Эти корни имеют разные знаки, причем положительный корень больше по абсолютной величине.
14.9. Если sin x ≥ 0 и cos x ≥ 0, то данное неравенство равносильно такому:
![]()
Так как при sin x ≥ 0 и cos x ≥ 0 имеем
sin x + cos x ≥ 1,
а при sin x > 0 и cos x > 0 это неравенство становится строгим, то отсюда следует, что неравенство (1) равносильно системе
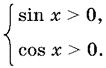
Ответ. 2nπ < x < π/2 + 2nπ.
14.10. Данное неравенство означает, что
π/4 + kπ ≤ 1/1 + x² < π/2 + kπ.
Если k > 0, то левое неравенство не имеет решений, поскольку 1/1 + x² не превосходит единицы. Если k < 0, то не имеет решений правое неравенство, так как 1/1 + x² — величина, положительная при всех x. Остается случай k = 0. При k = 0 правое неравенство удовлетворяется всегда. Решим левое неравенство.
![]()
Ответ.
![]()
14.11. Так как sin x + cos x = √2 cos (x − π/4), то, обозначив cos (π/4 − x) = y, получим неравенство
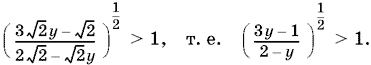
Это неравенство равносильно такому:
![]()
Так как y не превосходит 1, то 2 − y > 0. Поэтому y > ¾.
Решением неравенства cos (π/4 − x) > ¾ будут значения x − π/4, лежащие между 2kπ − arccos ¾ < x < 2kπ + arccos ¾.
Ответ. 2kπ + π/4 − arccos ¾ < x < 2kπ + π/4 + arccos ¾.
14.12. Перепишем неравенство в виде
![]()
Преобразуем знаменатель
cos x cos 3x = ½(cos 2x + cos 4x) = ½(cos 2x + 2 cos² 2x − 1)
и введем обозначение cos 2 x = y. Получим
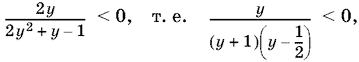
откуда y < −1, 0 < y < ½ и, наконец, 0 < cos 2x < ½.
Ответ: −π/4 + nπ < x < −π/6 + nπ; π/6 + nπ < x < /4 + nπ.
14.13. Пусть y = cos x, где |y| ≤ 1. Выражение 17/7 − cos x всегда положительно. Поэтому обе части данного неравенства можно возвести в квадрат; получим равносильное неравенство
![]()
Когда правая часть отрицательна, придем к системе
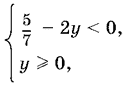
решением которой будут значения y > 5/14·
Когда правая часть неотрицательна, то получим другую систему
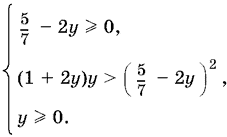
Второе неравенство этой системы можно переписать в виде
2 · 49у² − 7 · 27у + 25 < 0,
откуда
1/7 < y < 25/14, т. е. y > 1/7, так как y = cos x.
Решения всей системы будут лежать в интервале
1/7 < y ≤ 5/14
Объединяя его с интервалом y > 5/14, получим y > 1/7·
Ответ. −arccos 1/7 + 2nπ < x < arccos 1/7 + 2nπ.
14.14. Выразим sin x и cos x через tg x/2 и обозначим tg x/2 = y. Придем к неравенству
![]()
которое равносильно исходному. В самом деле, замена sin x и cos x их выражениями через tg x/2 может привести к потере решений, так как tg x/2 перестает существовать в тех точках, в которых sin x и cos x существуют Однако tg x/2 входит в первоначальное неравенство, а потому эти точки исключены с самого начала. Сокращение числителя и знаменателя на y² + 1, очевидно, не приводит ни к потере, ни к приобретению корней, так как y² + 1 ≠ 0 и y не исчез полностью из неравенства.
Неравенство относительно y перепишем в виде
![]()
После разложения левой части на множители получим
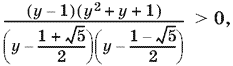
откуда
![]()
Находим интервалы изменения x:
![]()
Остается выделить решения, лежащие в интервале 0 < x < π.
Ответ.
![]()
14.15. Выразив sin 3α и cos 2α через sin α и обозначив sin α = y, получим
4(3y − 4у³) + 5 ≥ 4 − 8у² + 5у,
или
16у³ − 8у² − 7у − 1 ≤ 0.
Нетрудно заметить, что y = 1 — корень многочлена, стоящего в левой части неравенства. Теперь можно разложить этот многочлен на множители:
16у³ − 8у² − 7у − 1 = (y − 1)(4у + 1)².
Так как y = sin α, то y − 1 ≤ 0, а следовательно, и многочлен 16у³ − 8у² − 7y − 1 неположителен, что доказывает неравенство.
14.16. Значения x = πk, при которых sin x = 0, являются решениями неравенства при всех а > 0. На множестве остальных точек данное неравенство равносильно такому:
![]()
Так как
![]()
(сокращение на sin x правомерно, так как рассматриваются точки, в которых sin x ≠ 0), то приходим к неравенству:
(1 + 2cos 2x)² ≥ а².
Так как а > 0, то это неравенство распадается на два:
1 + 2cos 2x ≤ −а, 1 + 2cos 2x ≥ а,
т. е.
cos 2x ≤ −a + 1/2, cos 2x ≥ a − 1/2.
Первое имеет решения при − a + 1/2 ≥ −1, а второе — при a − 1/2 ≤ 1 или соответственно а ≤ 1 и а ≤ 3.
Найдем решение неравенства cos 2x ≤ −a + 1/2. Так как а > 0, то правая часть неравенства отрицательна и при а < 1 ему будут удовлетворять углы 2x, подвижные радиусы которых лежат в секторе, расположенном во второй и третьей четвертях симметрично горизонтальной оси (сделайте рисунок самостоятельно), т. е.
arccos (−a + 1/2) + 2πk ≤ 2x ≤ −arccos (−a + 1/2) + 2π + 2πk.
Так как arccos (−y) = π − arccos y, то
π − arccos a + 1/2 + 2πk ≤ 2x ≤ arccos a + 1/2 − π + 2π + 2πk.
Результат окончательных преобразований дан в ответе.
Ответ. При любом а > 0 y неравенства есть решения x = πk; при 0 < а ≤ 3 появляется вторая серия решений:
−½ arccos a − 1/2 + πk ≤ x ≤ ½ arccos a − 1/2 + πk;
при 0 < а ≤ 1 — третья серия:
−½ arccos a + 1/2 + π/2(2k + 1) ≤ x ≤ ½ arccos a + 1/2 + π/2(2k + 1).
14.17. Обозначим cos t = z и преобразуем условие задачи в неравенство
2z² + (2 cos x cos y)z + ½ cos² x cos² y + cos x − cos y > 0,
которое должно удовлетворяться при всех −1 ≤ z ≤ 1. Парабола, соответствующая трехчлену, стоящему в левой части неравенства, имеет абсциссу
z0 = −½ cos x cos y.
Следовательно, −1 < z0 < 1. Таким образом, условие задачи равносильно требованию, чтобы ордината этой вершины была положительна, что в свою очередь сводится к требованию отрицательности дискриминанта:
D = cos² x cos² y − cos² x cos² y − 2(cos x − cos y) < 0,
т. е.
cos x − cos y > 0, sin x + y/2 sin y − x/2 > 0. (2)
Нанесем на график точки, в которых
sin x + y/2 sin y − x/2 = 0.
Это будет совокупность прямых
x + y = 2πk, y − x = 2πn,
параллельных биссектрисам первого и второго координатных углов (рис. P.14.17), пересекающих оси координат в точках, координаты которых кратны 2π. Сами эти прямые не удовлетворяют неравенству (2), однако они разбивают всю плоскость на квадраты, внутри каждого из которых произведение sin y + x/2 sin y − x/2 сохраняет постоянный знак.
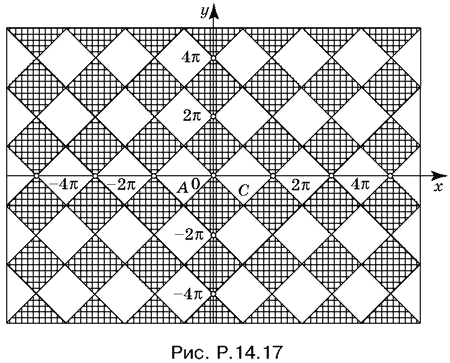
Рассмотрим квадрат ОАВС, примыкающий к началу координат снизу. Для всех внутренних точек этого квадрата
sin y + x/2 < 0 и sin y − x/2 < 0,
т. е. неравенство (2) удовлетворяется. При переходе через границу квадрата в любой точке, кроме вершины, произойдет смена знака одного из сомножителей. При переходе же через вершину знак поменяется дважды. Таким образом, вся плоскость окажется разбитой на области, расположенные в шахматном порядке. Те области, в которых неравенство (2) удовлетворяется, заштрихованы.
Ответ.