Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Решения
Трансцендентные уравнения
16.1. Из неравенства между средним арифметическим и средним геометрическим немедленно следует, что правая часть данного уравнения не меньше двух. Однако его левая часть не может стать больше двух. Поэтому остается лишь одна возможность:
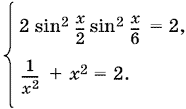
Последнее равенство достигается лишь при x² = 1, т. е. при x = ±1. Подставляя эти значения в левую часть первого уравнения, получим
2 sin² ½ sin² 1/6 < 2.
Таким образом, исходное уравнение не имеет решений.
16.2. Так как 1/cos² x = tg² x + 1, то уравнение можно переписать в виде
22 tg² x + 2 · 2tg² x − 80 = 0,
откуда
2tg² x = 8, tg² x = 3, tg x = ±√3, x = nπ ±π/3
(второе уравнение 2tg² x = −10 не имеет решений).
Ответ. nπ ±π/3.
16.3. Так как в условие одновременно входят tg x и etg x, то мы можем воспользоваться неабсолютным тождеством ctg x = 1/tg x, не опасаясь нарушения равносильности. Получим уравнение
(tg x)sin x = (tg x)−cos x.
Если tg x < 0, то sin x и cos x − дробные числа, и обе части равенства теряют смысл. При tg x = 0 и sin x обращается в нуль, т. е. левая часть теряет смысл.
Если tg x > 0, но ≠ 1, то sin x = −cos x, откуда tg x < 0, что противоречит сделанному предположению. Остается tg x = 1, x = (4k + 1)π/4.
Ответ. (4k + 1)π/4.
16.4. Данное уравнение можно записать так:
sin (2x + 2x − 1) = ½,
откуда
2x + 2x − 1 = nπ + (−1)n π/6, или 2x = 2nπ/3 + (−1)n π/9.
Какое бы положительное число ни стояло в правой части, уравнение будет иметь решение.
Неравенство
2nπ/3 + (−1)n π/9 > 0
выполняется при n ≥ 0.
Ответ. log2 [2nπ/3 + (−1)n π/9], где n ≥ 0.
16.5. Уравнение можно переписать так:
lg sin x + lg sin 5х + lg cos 4x = 0,
или в виде системы
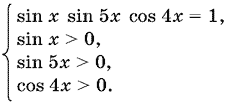
Из первого уравнения следует, что |sin x| = 1, |sin 5х| = 1, |cos 4x| = 1 одновременно. С учетом ограничений придем к системе
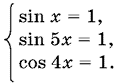
Из первого уравнения x = π/2 + 2πn. Подставляем во второе и третье уравнения:
sin [5(π/2 + 2πn)] = sin π/2 = 1, cos [4(π/2 + 2πn)] = cos 0 = 1.
Ответ. π/2 + 2πn.
16.6. Обозначив lg (sin x + 4) = y, получим уравнение
y² + 2y − 5/4 = 0,
y которого два корня: y1 = −5/2, y2 = ½.
Для первого корня получим
lg (sin x + 4) = −5/2,
откуда
![]()
Так как
![]()
то соответствующих значений x нет.
Для второго корня получим
lg (sin x + 4) = ½,
откуда
![]()
Так как
![]()
то можем найти x.
Ответ.
![]()
16.7. Данное уравнение эквивалентно системе
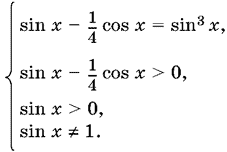
Уравнение можно преобразовать, если сгруппировать sin x и sin³ x:
sin x (1 − sin² x) − ¼ cos x = 0, или sin x cos² x − ¼ cos x = 0.
Так как sin x > 0, то cos² x < 1, и любое решение уравнения
sin x cos² x − ¼ cos x = 0
удовлетворяет неравенству
sin x − ¼ cos x > 0.
Запишем уравнение в виде
cos x(sin 2x − ½) = 0.
Так как sin x ≠ 1 и sin x > 0, то cos x ≠ 0. Остается
sin 2x = ½,
откуда
x1 = πn + π/12, x2 = (2n + 1)π/2 − π/12.
Из всех ограничений осталось удовлетворить только одному: sin x > 0. Чтобы добиться этого, нужно для x1 и x2 взять n = 2k.
Ответ. 2πk + π/12; 2πk + 5π/12.
16.8. Данное уравнение равносильно системе
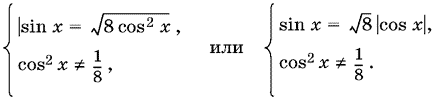
Условие sin x > 0 содержится в уравнении, так как справа стоит всегда неотрицательное число, а если cos x = 0, то sin x ≠ 0.
Рассмотрим следствие исходного уравнения
sin x = ±√8 cos x,
а в конце проверим выполнение условий: sin x > 0 и cos² x ≠ 1/8. Получим
tg x = ±√8, x = nπ + arctg √8.
Если tg x = ±√8, то tg² x + 1 = 9 и cos² x = 1/9 ≠ 1/8. Чтобы проверить выполнение условия sin x > 0, рассмотрим два случая.
Если n = 2k, то x = 2kπ ± arctg √8. Это — углы, лежащие в первой и четвертой четвертях; условие sin x > 0 выполняется лишь для тех из них, которые лежат в первой четверти: x1 = 2kπ + arctg √8.
Если n = 2k + 1, то x = 2kπ + π ± arctg √8. Здесь нужно выбрать знак минус, так как только тогда мы получаем угол, лежащий во второй четверти.
Ответ. 2kπ + arctg √8; (2k + 1)π − arctg √8.
16.9. Данное уравнение эквивалентно такому:
(½)x = 4k + 1/20.
Так как x > 0, то (½)x заключено между нулем и единицей. Следовательно, 0 < 4k + 1/20 < 1, откуда 0 ≤ k ≤ 4.
Для каждого из этих k находим соответствующее значение x.
Ответ. log2 20/4k + 1, где k = 0, 1, 2, 3, 4.
16.10. Решаем квадратное уравнение
![]()
Стоящее под корнем выражение неотрицательно, если −1 − √5 ≤ m ≤ −1 + √5.
Делаем следующий шаг:
![]()
Когда перед корнем взят минус, то стоящее справа положительное выражение не превзойдет единицы, а потому может быть косинусом. Когда перед корнем поставлен плюс, нужно, чтобы
![]()
После возведения в квадрат, учитывая полученные вначале ограничения для m, придем к системе
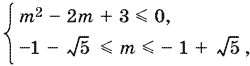
y которой два интервала решений:
−1 − √5 ≤ m ≤ −3, 1 ≤ m ≤ −1 + √5.
Ответ. При −1 − √5 ≤ m ≤ −1 + √5, x = 2nπ ± arccos A,
при −1 − √5 ≤ m ≤ −3 и 1 ≤ m ≤ −1 + √5, x = 2nπ ± arccos B, где
![]()
16.11. Решаем квадратное уравнение относительно lg sin x:
![]()
Подкоренное выражение должно быть неотрицательным: 2 а² − 2 ≥ 0, т. е. а ≤ −1, а ≥ 1.
Поскольку
![]()
то правая часть не должна превосходить единицу, а потому
![]()
Когда а ≥ 1, нужно рассмотреть лишь неравенство
![]()
откуда (с учетом ограничения а > 1) получаем а > √2. Если же а ≤ −1, то
![]()
всегда отрицательное число, а чтобы и число
![]()
было неположительно, должно быть еще а ≥ −√2.
Ответ. При а ≤ −√2
![]()
при −√2 ≤ а ≤ −1 и при а ≥ √2
![]()
при −1 < а < √2 решений нет.
16.12. Данная система равносильна такой:
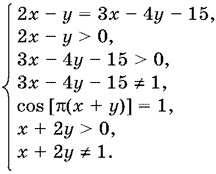
Решая входящие сюда два уравнения, получим
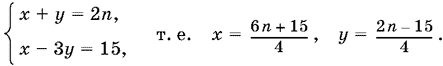
Из первого уравнения большой системы следует, что второе и третье неравенства выполняются одновременно. Поэтому достаточно потребовать
![]()
Аналогично убеждаемся, что условие 3x − 4у − 15 ≠ 1 выполняется при n ≠ −41/10, т. е. всегда, ибо n — целое.
Неравенство x + 2y > 0 справедливо при всех n > 1,5, т. е. n ≥ 2, а условие x + 2y ≠ 1 выполняется при n ≠ 1,9, т. е. всегда.
Ответ.
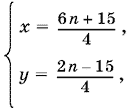
где n = 2, 3, 4, ... .
16.13. Если 4cos² πx = u, то
4sin² πx = 41 − cos² πx = 4/u.
Следовательно, левая часть уравнения обращается в 4/u + u, где u > 0. В силу неравенства, связывающего среднее арифметическое чисел u и 4/u со средним геометрическим этих же чисел, имеем
4/u + u ≥ 4.
Для оценки правой части уравнения выделим полный квадрат:
−8x² + 12|x| − ½ = −2( 2|x| − 3/2)² + 4 ≤ 4.
Поскольку левая часть уравнения не может стать меньше 4, в то время как правая его часть не может превзойти 4, остается проверить те два значения x = ±¾, при которых правая часть достигает своего наибольшего значения. Непосредственной проверкой убеждаемся, что x = ±¾ — корни данного уравнения.
Ответ. x = ±¾.
16.14. Запишем уравнение в виде
![]()
или
![]()
т. е.
![]()
Так как sin πx ≤ 1, а
![]()
то (1) имеет единственное возможное решение, когда обе части равенства равны 1. Правая часть равна 1 при x = 0,5. Вычислим sin πx при x = 0,5: sin 0,5π = sin π/2 = 1.
Ответ. 0,5.