Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Решения
Соединения и бином
21.1. Присвоим каждому из сидящих за круглым столом номер: а1, а2, ..., аn. Образовывая циклические перестановки: аn, а1, а2, ..., аn − 1; ап − 1, аn, а1, а2, ..., ап − 2 и т. д., мы будем получать тот же способ размещения за столом. Таких циклических перестановок можно составить n.
Кроме этого, нужно учесть, что сосед слева и сосед справа неразличимы, т. е. перестановки а1, а2, ..., ап и а1, аn, аn − 1, ..., а2 дают одно и то же размещение за столом. Так как всего возможно n! перестановок, из которых каждые 2n одинаковы, то искомое число равно
n!/2n = ½(n − 1)!.
Ответ. ½(n − 1)!.
21.2. Всего из пяти элементов можно составить Р5 перестановок. Среди них будет Р4, y которых на первом месте а1, и Р4, y которых на первом месте а2. Однако перестановки, y которых на первом месте а1, а на втором месте а2, попали и в первую, и во вторую группы. Таких перестановок Р3.
Поэтому искомое число перестановок равно
Р5 − (2P4 − Р3) = 78.
Ответ. 78.
21.3. Из семи разрядов три должны быть заняты двойками, что дает
![]()
вариантов. На каждое из оставшихся мест можно поместить любую из восьми цифр, благодаря чему каждый из предыдущих вариантов даст еще 84 возможностей.
Ответ.
![]()
21.4. Предположим, что в каждое число входят три различные единицы: l1, l2, l3, а остальные цифры 0, 2, 3, 4 и 5 равноправны. Тогда можно получить Р8 различных чисел. Отсюда нужно исключить Р7 чисел, начинающихся с нуля.
На самом деле разные единицы неразличимы. Другими словами, вместо одного числа мы получим Р3 одинаковых чисел, отличающихся лишь взаимными перестановками единиц.
Ответ.
![]()
21.5. Предположим, что каюты неравноценны. Это дает в 8! раз больше вариантов, чем в случае равноценных кают, что мы учтем позднее.
В первую каюту можно заселить любых четырех из 32 экскурсантов, что можно сделать
![]()
способами, во вторую — любых четырех из 28 оставшихся и т. д. В итоге получим
![]()
способов. Это число остается разделить на 8! и произвести упрощения.
Ответ.
![]()
.
21.6. Рассмотрим k−й член суммы
![]()
Данную сумму можно переписать в виде
![]()
Ответ. n · 2n − 1.
21.7. Из разложения
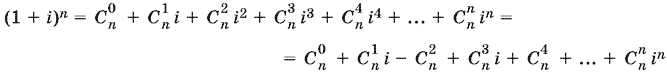
выделим действительную часть и приравняем действительной части комплексного числа (1 + i)n. В самом деле,
![]()
т. е.
![]()
где n − 1 ≤ 2k ≤ n.
Последнее ограничение означает, что через 2k обозначено то из чисел n − 1 и n, которое является четным.
Ответ.
![]()
21.8. Условию задачи удовлетворяют такие n, для которых равенство
![]()
выполняется хотя бы для одного k. Заметим, что 1 ≤ k ≤ n − 1; n ≥ 2. Равенство (1) перепишем в виде
![]()
что после простых преобразований даст
4k² − 4nk + п² − n − 2 = 0,
откуда
![]()
Чтобы выражение в правой части было целым, нужно сначала потребовать
n + 2 = m², т. е. n = m² − 2.
Поскольку n ≥ 2, то т² ≥ 4 и m ≥ 2. Тогда
![]()
Если взять знак минус, получим
![]()
Число, стоящее в числителе, четное при всех m. Значение m = 2 нужно исключить, так как тогда k1 = 0, что невозможно. Если же m ≥ 3, то m + 1 ≥ 4, а m − 2 ≥ 1. Следовательно, k1 ≥ 2. Потребуем теперь, чтобы выполнялось второе условие: k1 ≤ n − 1, т. е.
![]()
что равносильно неравенству m² + m − 4 ≥ 0. Последнее неравенство справедливо при всех m ≥ 3.
Остается исследовать
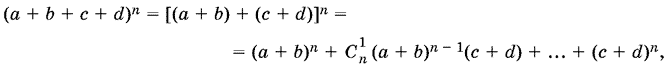
Так как условие n ≥ 2, из которого следует, что m ≥ 2, должно выполняться и для k2, то формула (3) по сравнению с (2) может дать лишь одно дополнительное значение: m = 2. Однако при m = 2 получим, что k2 = 2 и n = 2. Это противоречит требованию k ≤ n − 1. Таким образом, формула (3) не дает новых значений m, а следовательно, и n.
Ответ. n = m² − 2, где m = 3, 4, 5, ... .
21.9. Так как
(a + b + c + d)n = [(a + b) + (c + d)]n = (a + b)n + Cn1(a + b)n − 1(c + d) + ... + (c + d)n,
то после раскрытия скобок получим все неподобные члены. Их число будет равно
(n + 1) · 1 + n · 2 + (n − 1) · 3 + ... + 2n + 1(n + 1),
где для симметрии к крайним членам приписаны множителями единицы. Чтобы вычислить эту сумму, запишем ее k−й член: (n + 2 − k) = (n + 2)k − k². Тогда наша сумма примет вид
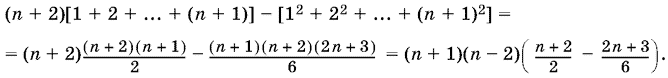
Ответ.
![]()
21.10. Предположим, что 0 ≤ k ≤ n − 1. Запишем данное выражение в виде
(1 + x + x² + ... + xk − 1 + xk + xk + 1 + ... + xn − 1)².
Члены, содержащие xk, могут быть получены только в результате почленного перемножения членов суммы 1 + x + x² + ... + xk − 1 + xk с членами той же суммы, записанной в обратном порядке, т. е.
1 · хk, x · хk − 1, ..., хk − 1 · x, xk · 1
Так как слагаемых будет k + 1, то и коэффициент при xk будет равен k + 1.
Предположим теперь, что n − 1 < k ≤ 2(n − 1). Тогда нужно почленно перемножить суммы
xk − n + 1 + ... + xn − 1, xn − 1 + ... + xk − n + 1,
в результате чего получим 2n − k − 1 членов, содержащих xk.
Ответ. k + 1, если 0 ≤ k ≤ n − 1;
2n − k − 1, если n − 1 < k ≤ 2n − 2.
21.11. Сравним коэффициент члена разложения с номером k + 1 с коэффициентом десятого члена разложения:
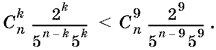
Так как знаменатели одинаковы, то
![]()
Поскольку десятый член разложения имеет наибольший коэффициент, то он больше девятого и больше одиннадцатого:
![]()
Из первого неравенства следует, что
![]()
Из второго
![]()
Ответ. n = 13.
21.12. Преобразуем выражение, стоящее в левой части, следующим образом:
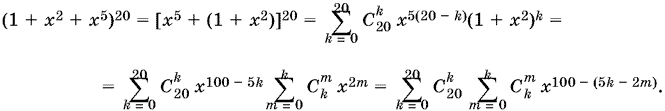
Вопрос состоит в следующем: если k, m = 1, 2, ..., 20, причем m ≤ k, то какие значения от 0 до 100 принимает выражение 5k − 2m.
Если m = 0, 1, 2, 3, 4, то получим соответственно 5k, 5k − 2, 5k − 4, 5k − 6, 5k − 8. Если бы k не было связано ограничениями, то мы получили бы все числа, так как в эти пять выражений вошли числа, дающие при делении на 5 в остатке 0, 3, 1, 4 и 2 соответственно. Однако k = 0, 1, ..., 20 и, кроме того, k ≥ m. Так как 5k получено при m = 0, то k может принимать все свои 21 значение, в результате чего получим все числа, кратные 5 от 0 до 100. Рассмотрим теперь числа, которые при делении на 5 дают в остатке 1. У нас они записаны в виде 5k − 4 и получились при m = 2, в силу чего k = 2, 3, ..., 20. В результате мы получим 19 чисел, дающих при делении на 5 в остатке 1. В эту группу не войдет лишь число 1. Числа, дающие в остатке 2, записаны в виде 5k − 8, где k ≥ 4. Следовательно, 5k − 8 = 12, 17, ..., 92, т. е. выпадают числа 2, 7 и 97. Для чисел вида 5k − 2 переменная k = 1, 2, ..., 20 и 5k − 2 = 3, 8, ..., 98, куда вошли все числа, дающие в остатке 3. Среди чисел вида 5k − 6, где k = 3, ..., 20, мы не встретим 4 и 99.
Числа 1, 2, 4, 7, 97 и 99 не могут быть получены из выражения 5k − 2m и при m > 4. В самом деле, с одной стороны, 5k − 2m ≥ 5m − 2m = 3m > 12, а с другой стороны,
5k − 2m < 5k − 8 ≤ 100 − 8 = 92,
т. е.
12 < 5k − 2m < 92.
Итак, выпали 6 чисел 1, 2, 4, 7, 97 и 99, т. е. будут отсутствовать члены с показателями 99, 98, 96, 93, 3, 1.
Ответ. 95.
21.13. Пусть Рn — ответ на вопрос задачи для последовательности, состоящей из n элементов. В первой группе может оказаться либо один элемент (а1), либо два элемента (а1, а2). Разбиений, содержащих в первой группе один элемент (а1), будет столько, сколько разбиений можно образовать из n − 1 оставшихся членов последовательности а2, а3, ..., аn, т. е. Рn − 1. Разбиений же, содержащих в первой группе два элемента, будет Рn − 2, так как после образования группы (а1, а2) останется n − 2 элементов а3, ..., аn.
Итак
Рn = Рn − 1 + Рn − 2.
Такая формула называется рекуррентной, потому что, зная Р1 и Р2 и применяя ее последовательно, мы получим Р3, затем Р4 и т. д. Поскольку Р1 = 1, а Р2 = 2, то Р3 = 3, Р4 = 5, Р5 = 8, Р6 = 13, Р7 = 21, Р8 = 34, Р9 = 55, Р10 = 89.
Ответ. 89.
21.14. Пусть на плоскости проведены m параллельных прямых. Они разобьют ее на m + 1 областей. Если провести еще одну непараллельную прямую, то областей станет 2(m + 1). Предположим, что k непараллельных прямых образуют, пересекаясь с m параллельными прямыми, Мk областей. Если добавить еще одну прямую, пересекающую все имеющиеся, но не проходящую ни через одну из старых точек пересечения, то на этой прямой будет m + k точек пересечения с остальными прямыми, в результате чего образуется m + k + 1 новых областей.
Таким образом,
Мk + 1 = Мk + m + k + 1.
Так как Мо = m + 1, то
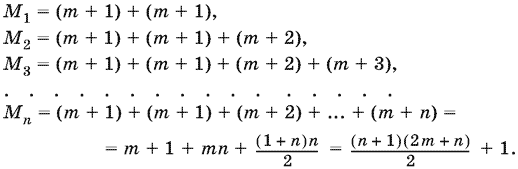
Остается доказать эту формулу методом математической индукции, что сводится к элементарным выкладкам, которые мы оставляем читателю.
Ответ.
![]()