Вариант № 15 - Учебно-тренировочные тесты - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ

Часть 1

В1. В доме, в котором живёт Петя, один подъезд. На каждом этаже находится по 5 квартир. Петя живёт в квартире № 37. На каком этаже живёт Петя?

В2. На графике (рис. 92) показано изменение удельной теплоёмкости водного раствора некоторого вещества в зависимости от температуры. По горизонтали указывается температура в градусах Цельсия, по вертикали — удельная теплоёмкость в Определите по рисунку наименьшую возможную удельную теплоемкость раствора в диапазоне температур от 20° до 90°. Ответ дайте в

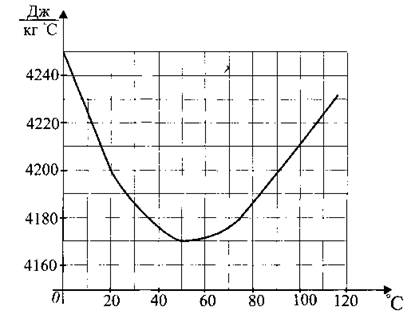
Рис. 92.

В3. На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 9п. Найдите площадь заштрихованной фигуры. В ответе запишите результат (см. рис. 93).

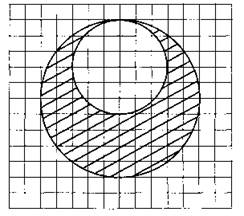
Рис. 93.

В4. Своему постоянному клиенту компания сотовой связи решила предоставить на выбор одну из скидок: либо скидку 30% на звонки абонентам других сотовых компаний в своём регионе, либо скидку 10% на звонки в другие регионы, либо скидку 20% на услуги мобильного Интернета. Клиент проанализировал распечатку своих звонков и выяснил, что за месяц он потратил 400 рублей на звонки абонентам других компаний в своём регионе, 600 рублей на звонки в другие регионы и 500 рублей на мобильный Интернет. Клиент предполагает, что в следующем месяце затраты будут такими же, и, исходя из этого, выбирает наиболее выгодную для себя скидку. Сколько рублей составит эта скидка, если звонки и пользование Интернетом сохранятся в прежнем объёме?

В5. Найдите корень уравнения log₃ (4 + х) = log₃ 4.

В6. В треугольнике АВС угол С равен 90°, СН — высота, АВ = 18, sin ∠А = 1/3. Найдите ВН.

В7. Найдите значение выражения

В8. Прямая у = —8х + 1 параллельна касательной к графику функции у = 2х² — 2х + 9. Найдите абсциссу точки касания.

В9. Шар вписан в цилиндр (см. рис. 94). Площадь поверхности шара равна 18. Найдите площадь полной поверхности цилиндра.

Рис. 94.

В10. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 4, но не дойдя до отметки 7 часов.

В11. В сосуд, имеющий форму правильной треугольной призмы, налили воду (см. рис. 95). Уровень воды достигает 18 см. На какой высоте будет находиться уровень воды, если её перелить в другой такой же по форме сосуд, у которого сторона основания в 3 раза больше, чем у первого? Ответ выразите в см.

Рис. 95.

В12. Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полёта камня описывается формулой у = ах² + bх, где а = -1/100 м^-1, b = 1 — постоянные параметры, х (м) — смещение камня по горизонтали, у (м) — высота камня над землёй. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 14 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 2 метров?

В13. Баржа в 8:00 вышла из пункта А в пункт В, расположенный в 21 км по реке от пункта А. Пробыв в пункте В 1 час, баржа отправилась назад и вернулась в пункт А в 16:00. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи 8 км/ч.

В14. Найдите наименьшее значение функции у = 4x — ln (4х + 2) — 8.

Часть 2

С1. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие промежутку (5π/6; 3π].

С2. Боковые рёбра правильной четырёхугольной пирамиды наклонены к плоскости основания под углом α, Под каким углом наклонены к плоскости основания боковые грани пирамиды?

С3. Решите неравенство log₃ х + log_x 3 > 2.

С4. Расстояние от центра описанной окружности равнобедренного треугольника до его основания равно 3. Найдите боковую сторону этого треугольника, если его основание равно 8.

С5. Найдите все значения параметра а, при каждом из которых уравнение (а — 1)х² + (2a + 3)х + a = 0 имеет два различных корня и только меньший из корней принадлежит промежутку (—2; 3].

С6. а) Какое наименьшее количество клеток нужно закрасить в квадрате 8x8, чтобы в каждом квадрате 3x3 была ровно одна закрашенная клетка? Какое наибольшее количество клеток можно закрасить указанным образом?

б) Если m ≥ k, то какое наименьшее количество клеток нужно закрасить в квадрате mхm, чтобы в каждом квадрате kхk была ровно одна закрашенная клетка?

в) А какое наибольшее количество (для условий пункта б)?