Треугольник - Планиметрия - Геометрия - Базовый уровень

667. В треугольнике АВС точка D делит сторону АС на отрезки AD = 4 и DC = 5, ABAC = 30°, ∠ABD = ∠ACВ. Найдите площадь треугольника ABD.

668. В равнобедренном треугольнике АВС угол при вершине В равен 120°. Расстояние от точки М, лежащей внутри треугольника, до основания треугольника равно 1/√3, а до боковых сторон равно 3. Найдите АС.

669. В треугольнике АВС сторона ВС равна 2√97, и она больше половины стороны АС. Найдите сторону АВ, если медиана ВМ равна 12, а площадь треугольника АВС равна 96.

670. В треугольнике АВС сторона АВ равна 10, угол А — острый. Найдите медиану ВМ, если АС = 20, а площадь треугольника АВС равна 96.

671. На сторонах АВ и ВС треугольника АВС взяты соответственно точки М и N так, что AM : МВ = 3 : 4 и BN : NC = 3:5. Найдите площадь треугольника АВС, если площадь треугольникаMNA равна 9.

672. На сторонах АВ и ВС треугольника АВС взяты соответственно точки М и N так, что AM : МВ = 2 : 3 и BN : NC = 4:9. Найдите площадь четырёхугольника AMNC, если площадь треугольника АВС равна 130.

673. В треугольнике АВС на стороне АС взята точка D так, что длина отрезка AD равна 3, косинус угла ВDC равен 13/20, а сумма углов АВС и ADB равна π. Найдите периметр треугольника АВС, если длина стороны ВС равна 2.

674. Отрезки КР и МН имеют равные длины и пересекаются в точке О так, что КН || МР, ОН = 4, ОМ = 5. Найдите отношение периметров треугольников ОКМ и ОНР. Отрезки КР и МHимеют равные длины и пересекаются в точке О так, что КН || МР, ОН = 4, ОМ = 5. Найдите отношение периметров треугольников ОКМ и ОНР.

675. В треугольнике АВС медианы АО и BE пересекаются под прямым углом. Найдите сторону АВ этого треугольника, если АС = 30 и ВС = 12√5.

676. Дан треугольник АВС. Известно, что АС = 10, ВС = 12 и ∠CAB = 2∠CBA. Найдите длину стороны АВ.

677. В треугольнике АВС с тупым углом В и со стороной ВС длиной 5 проведена биссектриса BD. Площади треугольников ABD и BCD равны соответственно Найдите длину стороны АС.

678. В равнобедренном треугольнике длина основания равна 6, а диаметр вписанной окружности равен 2. Найдите радиус описанной около данного треугольника окружности.

679. В равнобедренном треугольнике АВС с основанием ВС высоты ВВ₁ и CC₁ пересекаются в точке М, при этом АВ₁ = 24, BB₁ = 32. Найдите площадь треугольника АВМ.

680. В равнобедренном треугольнике КЕМ с основанием КМ высоты LP и КВ пересекаются в точке О. Найдите площадь треугольника KLO, если LO = 5, РО = 4.

681. В ∆ABC ∠A = 30°, точка О — центр вписанной в А АВС окружности. Прямые АО и ВО пересекают описанную вокруг ААВС окружность в точках М и N соответственно. Найдите величину угла С в градусах, если известно, что AM = MN.

682. В равнобедренном треугольнике биссектриса, проведённая к боковой стороне, делит её в отношении 5:8, считая от вершины. Найдите длину основания данного треугольника, если радиус его вписанной окружности равен 2.

683. В равнобедренном треугольнике АВС с равными сторонами АС и СВ и углом при вершине (7, равным 120°, проведены биссектрисы AM и BN, равные 5. Найдите площадь четырёхугольника AN МВ.

684. В равнобедренном треугольнике АВС с равными сторонами АС и СВ и углом при вершине (7, равным 120°, проведены биссектрисы AM и BN. Найдите длину биссектрисы BN, если площадь четырёхугольника AN МВ равна 12,25.

685. В прямоугольном треугольнике АВС с прямым углом В проведена биссектриса CD. Найдите площадь треугольника ACD, если СВ = 6, BD = 3.

686. В треугольнике АВС проведена биссектриса AD угла ВАС, равного 60°. Известно, что ВС = 6, CD = 2. Определите градусную меру угла АВС.

687. В равнобедренном треугольнике с острым углом при вершине боковая сторона равна 25, а его площадь равна 300. Найдите основание треугольника.

688. Биссектриса AM треугольника АВС делит сторону СВ на отрезки СМ = 10 и МВ = 14. АВ равно 21√2. Найдите радиус описанной вокруг А АВС окружности.

689. На координатной плоскости заданы точки А(—1; 3), В(2; —3), C(—1; —4). Вычислите площадь треугольника АВС.

690. На координатной плоскости заданы точки A(0; 1), В(3; 2), C(3; 5). Вычислите площадь треугольника АВС.

691. В равнобедренном треугольнике РКМ с основанием РМ боковая сторона РК равна 13, a cos P = √105/13. Найдите высоту, проведённую к основанию.

692. В треугольнике АВС угол С равен 90°, cos A = 3/5, АВ = 20. Найдите ВС.

693. В треугольнике АВС угол С равен 90°, cos В = 4/5, АВ = 15. Найдите АС.

694. В треугольнике АВС угол С равен 90°, АВ = 10, ВС = 8. Найдите cos А.

695. В треугольнике АВС угол С равен 90°, АВ = 29, ВС = 21. Найдите tg А.

696. В треугольнике АВС АВ = 8, ∠A = ∠В, cos А = 4/5. Найдите биссектрису СН.

697. В треугольнике АВС АС = ВС = 10, cos А = 0,6. Найдите площадь треугольника АВС.

698. В равнобедренном треугольнике АВС с основанием АС боковая сторона равна 22, a cos С = 4√6/11. Найдите высоту, проведённую к основанию.

699. В равнобедренном треугольнике АВС с основанием АС боковая сторона АВ равна 8, а высота, проведённая к основанию, равна 3√7. Найдите косинус угла А.

700. В прямоугольном треугольнике ABC ZC = 90°, АВ = √13, АС = 3. Найдите ctg ∠А.

701. В треугольнике ABC ∠C = 90°, АС = 3, ВС = 3√3. Найдите sin ZB.

702. В треугольнике ABC ∠C = 90°, sin Б = 0,2, ВС = 6√6. Найдите АС.

703. В прямоугольном треугольнике АВС с прямым углом С АВ = 25, cos А = 0,28. Найдите ВС.

704. В треугольнике АВС АС = ВС, АВ = 10, sin A = 12/13. Найдите высоту СН.

705. В треугольнике ABC ∠C = 90°, АВ = 12,5, ВС = 12. Найдите косинус внешнего угла при вершине А.

706. В прямоугольнике ABCD сторона АВ = 1,6, а диагональ прямоугольника равна 2. Найдите синус угла ACD.

707. В тупоугольном треугольнике АВС АВ = ВС, СН — высота, АВ = 2,5, ВН = 2. Найдите косинус угла АВС.

708. В тупоугольном треугольнике АВС АВ = ВС, АВ = 13, высота СН равна 5. Найдите котангенс угла АВС.

709. В треугольнике АВС АВ = ВС, АС = 26, СН — высота, АН = 10. Найдите тангенс угла АСВ.

710. В треугольнике ABC ∠C = 90°, СН — высота, ВС = 8, ВН = 2√7. Найдите cos ∠A.

711. В треугольнике АВС (см. рис. 291) угол В равен 90°, ВС = 5, tg ∠C = 2,4. Найдите АС.

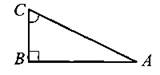
Рис. 291.

712. В треугольнике АВС угол С равен 90°, cos ∠B = √15/4. Найдите синус внешнего угла при вершине В.

713. В равнобедренном треугольнике АВС с основанием АС боковая сторона АВ = 10, cos ∠A = √3/2. Найдите высоту, проведённую к основанию.

714. В треугольнике АВС АС = ВС = 16, sin ∠B = 3√23/16. Найдите АВ.

715. В треугольнике АВС угол С равен 90°, sin ∠A = 7/36, АВ = 144. Найдите ВС.

716. В треугольнике АВС угол С равен 90°, АВ = √74, АС = 5. Найдите котангенс угла В.

717. В тупоугольном треугольнике АВС АВ = ВС, АС = 8, высота СН = √28. Найдите косинус угла АСВ.

718. В треугольнике АВС угол С равен 90°, sin А = 0,2, АС = 6√6. Найдите ВС.

719. В треугольнике АВС угол С равен 90°. Найдите синус внешнего угла при вершине A, если tg А = 4/3.

720. В равнобедренном треугольнике боковая сторона равна 3, а косинус угла при вершине равен —0,28. Найдите радиус вписанной в него окружности.

721. В треугольнике АВС угол С равен 90°, ВС = 5, tg А = √21/2. Найдите высоту СВ.

722. В треугольнике АВС угол С равен 90°, СН — высота, ВС = 8, sin А = 1/4. Найдите АН.

723. Боковая сторона равнобедренного треугольника равна 9 (см. рис. 292). Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма CLDK.

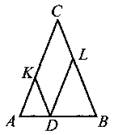
Рис. 292.

724. В треугольнике АВС АС = СВ, АН — высота, sin ∠BAC = 0,2. Найдите cos ∠ВАН.

725. В треугольнике АВС АС = ВС = 9, cos А = 4/5. Найдите высоту СН.

726. В треугольнике АВС угол А равен 64°, угол В равен 80°. AL, BN и СК — биссектрисы, пересекающиеся в точке О (см. рис. 293). Найдите угол АОК. Ответ дайте в градусах.

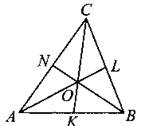
Рис. 293.

727. Острые углы прямоугольного треугольника равны 38° и 52°. Найдите угол между высотой и медианой, проведёнными из вершины прямого угла (см. рис. 294). Ответ дайте в градусах.

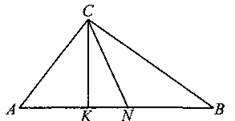
Рис. 294.

728. Сумма двух углов треугольника и внешнего угла к третьему равна 70°. Найдите третий угол треугольника. Ответ дайте в градусах.

729. В треугольнике АВС угол С равен 90°, АВ = 30, АС = 18. Найдите синус внешнего угла при вершине А.