Задачи на построение сечений - ТЕТРАЭДР. ПАРАЛЛЕЛЕПИПЕД - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

Цель урока:

- выработать навыки решения задач на построение сечений тетраэдра и параллелепипеда.

Ход урока

I. Организационный момент

II. Проверка домашнего задания

Ответы на вопросы 14, 15.

14. Существует ли тетраэдр, у которого пять углов граней прямые? (Ответ: Нет, так как граней всего 4, они являются треугольниками, а треугольника с двумя прямыми углами не существует.)

15. Существует ли параллелепипед, у которого: а) только одна грань - прямоугольник; б) только две смежные грани - ромбы; в) все углы граней острые; г) все углы граней прямые; д) число всех острых граней не равно числу всех тупых углов граней?

(Ответ: а) нет (противоположные грани равны); б) нет (по той же причине); в) нет (таких параллелограммов не существует); г) да (прямоугольный параллелепипед); д) нет (в каждой грани два острых и два тупых угла, либо все прямые.)

III. Изучение нового материала

План:

1. Теоретическая часть.

2. Практическая часть (решение задачи № 1).

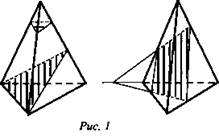
Учитель: 1) для решения многих геометрических задач, связанных с тетраэдром и параллелепипедом, полезно уметь строить на рисунке их сечения различными плоскостями. Под сечением будем понимать любую плоскость (назовем ее секущей плоскостью), по обе стороны от которой имеются точки данной фигуры (то есть тетраэдра или параллелепипеда). Секущая плоскость пересекает тетраэдр (параллелепипед) по отрезкам. Многоугольник, который будет образован этими отрезками, и является сечением фигуры. Так как тетраэдр имеет четыре грани, то его сечением могут быть треугольники и четырехугольники (рис. 1). Параллелепипед имеет шесть граней. Его сечением могут быть треугольники (рис. 2 а), четырехугольники (рис. 2 б), пятиугольники (рис. 2 в) и шестиугольники (рис. 2 г).

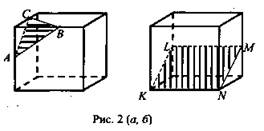
При построении сечения параллелепипеда учитываем тот факт, что если секущая плоскость пересекает две противоположные грани по каким-то отрезкам, то эти отрезки параллельны (свойство 1, п. 11: Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны). Более подробно с построением сечения параллелепипеда мы познакомимся на следующем уроке.

Для построения сечения достаточно построить точки пересечения секущей плоскости с ребрами тетраэдра (параллелепипеда), после чего остается провести отрезки, соединяющие каждые две построенные точки, лежащие в одной и той же грани.

2) Рассмотрим примеры построения различных сечений тетраэдра, для этого решим задачу: На ребрах АВ, BD и CD тетраэдра ABCD отмечены точки М, N, Р (рис. 3 а). Построить сечение тетраэдра плоскостью MNP.

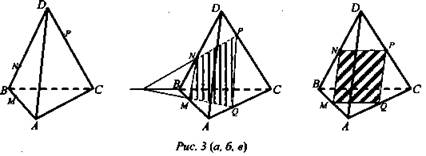
Решение: Построим сначала прямую, по которой плоскость MNP пересекается с плоскостью грани ABC. Точка М является общей точкой этих плоскостей. Для построения еще одной общей точки продолжим отрезки NP и ВС до их пересечения в точке Е (рис. 3 б), которая и будет второй общей точкой плоскостей MNP и ABC. Следовательно, эти плоскости пересекаются по прямой ME. Прямая ME пересекает ребро АС в некоторой точке А. Четырехугольник MNPQ - искомое сечение.

Если прямые NP и ВС параллельны (рис. Зв), то прямая NP параллельна грани ABC, поэтому плоскость MNP пересекает эту грань по прямой ME, параллельной прямой NP. Точка Q, как и в предыдущем случае, есть точка пересечения ребра АС с прямой ME.

3) Работа у доски:

- Первый ученик: построить сечение тетраэдра DABC плоскостью, проходящей через данные точки MNK.

- Второй ученик: построить сечение тетраэдра МКРН плоскостью, проходящей через точки ABC. Найти периметр Сечения. Ребро тетраэдра равно а.

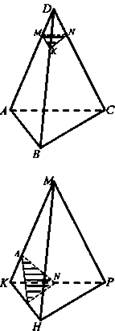
- Третий ученик (№ 105): Изобразите тетраэдр DABC и отметьте точки M и N на ребрах BD и CD и внутреннюю точку К грани ABC. Постройте сечение тетраэдра плоскостью MNK.

Решение: Обозначим секущую плоскость буквой α. Тогда

Возможны два случая:

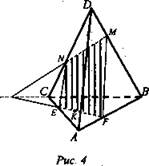
1°) MN ∩ ВС = Р; 2°) MN || BС. Рассмотрим их отдельно. 1°) Проводим прямую MN. Проводим прямую РК. Пусть она пересекает стороны АС и АВ в точках Е и F. Проводим отрезки NE и MF. Искомое сечение - четырехугольник MNEF (рис. 4).

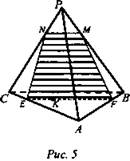
2) Через точку К проводим EF || ВС. Проводим отрезки NE и MF. Искомое сечение - четырехугольник MNEF (рис. 5).

3) Работа по карточкам: (пока третий ученик работает у доски, 4 ученика работают по карточкам).

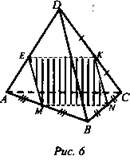
- построить сечение тетраэдра DABC плоскостью, проходящей через данные точки М, N, К. Найти периметр сечения. Ребро тетраэдра равно а (рис. 6).

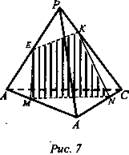
- построить сечение тетраэдра DABC плоскостью, проходящей через данные точки М, N, К; NM || АС (рис. 7).

- построить сечение тетраэдра DABC плоскостью, проходящей через данные точки М, N, К. EKNM - искомое сечение (рис. 8).

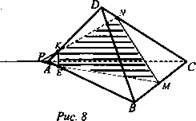
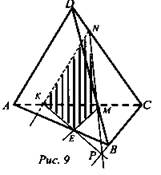
- построить сечение тетраэдра DABC плоскостью, проходящей через данные точки М, N, К (рис. 9). KNME - искомое сечение.

Домашнее задание

П. 14, стр. 27 № 104 - Вариант I, № 106 - Вариант II.

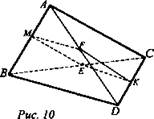
Задача 104

Решение: Проведем ME || АС и MF || BD. По теореме 2. (Через две пересекающие прямые проходит плоскость, и притом только одна) плоскость сечения пересечет плоскость BCD по прямой, параллельной MF (MF || плоскости BCD по построению), значит, проводим ЕК || BD. Соединим точки К и F. Четырехугольник MEKF - искомое сечение. Докажем это. АС || плоскости MEF (так как АС || ME; ME ⊂ MEF). BD || плоскости MEF (то есть BD || MF; MF ⊂ MEF). Итак, плоскость MEKF || AC и плоскость MEKF || BD. Так как через точку М можно провести лишь одну прямую ME || АС в плоскости грани ABC и одну прямую MF || BD в плоскости грани BAD, то плоскость MEKF - единственная, удовлетворяющая условию задачи (рис. 10).

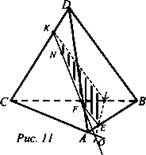
Задача 106

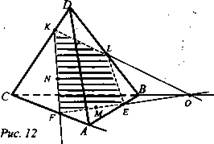
Решение: Пусть точки расположены так, как показано на рисунке 11. 1. Проводим KN до пересечения с продолжением ребра СА. Пусть KN пересечет СА в точке О. 2. Проводим луч ОМ; он пересечет ребро АВ в точке Е, а ребро ВС - в точке L. Соединим К и L, F и Е (точка F - точка пересечения KN с ребром DA). Сечение KFEL - искомое.

Построим:

1) KN до пересечения в точке F с ребром АС.

2) FM до пересечения с ребром АВ в точке Е и ребром ВС (его продолжением) в точке О.

3) ОК, он пересечет DB в точке L.

4) отрезок EL.

5) KFEL - искомое сечение (рис. 12).

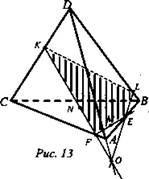
Проводим KN до пересечения с АС в точке F; продолжаем KN за точкой F до пересечения с продолжением DA в точке О; FM до пересечения с АВ в точке Е; ОЕ до пересечения с DB в точке L; отрезок KL. KFEL - искомое сечение (рис. 13).

VII. Подведение итогов

Оценки.