Поурочные разработки по геометрии 10 класс
Задачи на построение сечений - урок 2 - ТЕТРАЭДР. ПАРАЛЛЕЛЕПИПЕД - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цель урока:
- выработать навыки решения задач на построение сечений параллелепипеда.
Ход урока
I. Организационный момент
II. Проверка домашнего задания
Вопрос: Какие многоугольники могут получиться в сечении
а) тетраэдра; б) параллелепипеда? Ответ: а) треугольники и четырехугольники; б) треугольники, четырехугольники, пятиугольники, шестиугольники. № 104, 106 (решение см. в плане урока № 20).
III. Изучение нового материала
Задача № 3
На ребрах параллелепипеда даны три точки А, В, С. Построить сечение параллелепипеда плоскостью ABC.
Решение:
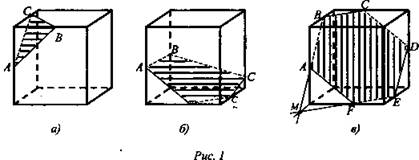
Построение искомого сечения зависит от того, на каких ребрах параллелепипеда лежат точки А, В, С. В самом простом случае, когда эти точки лежат на ребрах, выходящих из одной вершины (рис. 1 а), нужно провести отрезки АВ, ВС, СА, и получится искомое сечение - треугольник ABC. Если три точки А, В, С расположены так, как показано на рис. 1 б, то сначала нужно провести отрезки АВ и ВС, а затем через точку А провести прямую, параллельную ВС, а через точку С - прямую, параллельную АВ. Пересечения этих прямых с ребрами нижней грани дают точки Е и D. Остается провести отрезок ED, и искомое сечение - пятиугольник ABCDE.
Более трудный случай, когда данные точки А, В, С расположены так, как показано на рис. 1 в. В этом случае поступим так. Сначала построим прямую, по которой секущая плоскость пересекается с плоскостью нижнего основания. Для этого проведем прямую АВ и продолжим нижнее ребро, лежащее в той же грани, что и прямая АВ, до пересечения с этой прямой в точке М. Далее через точку М проведем прямую, параллельную прямой ВС. Эго и есть прямая, по которой секущая плоскость пересекается с плоскостью нижнего основания. Эта прямая пересекается с ребрами нижнего основания в точках Е и F. Затем через точку Е проведем прямую, параллельную прямой АВ, и получим точку D. Наконец, проводим отрезки AF и CD, и искомое сечение - шестиугольник ABCDEF - построено.
IV. Работа у доски
- первый ученик:
Задача 79
а) Решение: плоскость ВВ1С1С || AA1D1 по свойству параллелепипеда, отсюда ВС1 || AA1D1. Точка А общая для плоскостей ABC1 и AA1D1 - плоскости пересекаются по прямой, проходящей через точку А и параллельной ВС1. (Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны), очевидно, это AD1. Искомое сечение - четырехугольник ABC1D1.
Доказательство: АВ || CD (так как ABCD - параллелограмм). АВ = CD (так как ABCD - параллелограмм). CD || C1D1 (так как CDD1C1 - параллелограмм). CD - C1D1 (так как CDD1C1 - параллелограмм).
Отсюда следует, что АВ || C1D1. Значит, ABC1D1 - параллелограмм, так как его противоположные стороны параллельны и равны.
- второй ученик:
Задача 8.
Решение:
а) Сечение плоскостью АВС1. Плоскость ВВ1C1 || AA1D1 по свойству параллелепипеда, отсюда ВС1 || AA1D1D. Тогда А - общая точка для плоскостей АВС1 и AA1D1 - плоскости пересекаются по прямой, проходящей через точку А и параллельной ВС1. (Свойство см. в предыдущей задаче). Плоскости граней AA1B1B и DD1C1C пересечены плоскостью АВС1, значит, их линии пересечения параллельны, АВ || C1D1.
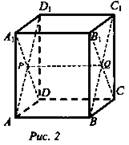
Вывод: плоскость пересекает грань AA1D1D по прямой AD1 AD1 || ВС1. Искомое сечение ABC1D1 параллелограмм по определению.
б) Сечение плоскостью DCB1. Точка D - общая для плоскостей DCB1 и AA1D - плоскости пересекаются по прямой DA1, (свойство 1 из п. 11). В плоскости грани AA1D1D проводим такую прямую. Это будет DA1 (четырехугольник DCB1A1 - параллелограмм, поэтому DA1 || СВ1), искомое сечение DCB1A1.
в) PQ - отрезок, по которому пересекаются построенные сечения (Р принадлежит плоскости сечений и Q принадлежит плоскостям сечений, PQ - линия пересечения плоскостей), где Р и Q - центры граней AA1D1D и BB1C1C.
V. Работа по карточкам (S учащихся работают по карточкам самостоятельно, один у доски).
Карточка № 1
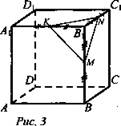
Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами его ребер (три данные точки на рисунке выделены). Найти периметр сечения, если ребро куба равно а (рис. 3).
Карточка № 2
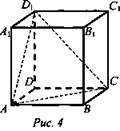
Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся вершинами куба (три данные точки на рисунке выделены). Найти периметр сечения, если ребро куба равно а (рис. 4).
Карточка № 3
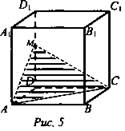
Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся либо вершинами куба, либо серединами его ребер (три данные точки на рисунке выделены). Найти периметр сечения, если ребро куба равно а (рис. 5).
Карточка № 4
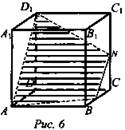
Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся либо вершинами куба, либо серединами его ребер (три данные точки на рисунке выделены). Найти периметр сечения, если ребро куба равно а (рис. 6).
Карточка № 5
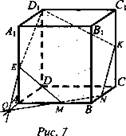
Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся либо вершинами куба, либо серединами его ребер (три данные точки на рисунке выделены). Доказать, что ![]() (ребро куба равно а) (рис. 7).
(ребро куба равно а) (рис. 7).
Карточка № 6
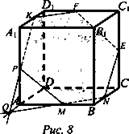
Построить сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами его ребер (три данные точки на рисунке выделены) (рис. 8).
Карточка № 7
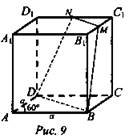
Все грани параллелепипеда - равные ромбы со стороной а и острым углом 60°. Построить сечение параллелепипеда плоскостью, проходящей через точки В, D, М, если М - середина ребра ВС. Доказать, что построенное сечение есть равнобедренная трапеция. Найти стороны трапеции.
Решение:
1) Пусть α - секущая плоскость, α ∩ ABC = BD, α ∩ BCC1B1 = ВМ, MN || BD, сечение - трапеция BDNM.
2) ΔBB1M = ΔDD1N, ВМ = DN, трапеция BDNM равнобедренная.
3) ![]() (домашнее задание для более сильных учащиеся) (рис. 9).
(домашнее задание для более сильных учащиеся) (рис. 9).
Домашнее задание
П. 14, № 196 - первый вариант, № 81 - второй вариант, № 87 – третий вариант.
Задача 79 б)
Решение: Сечение плоскостью АСС1. Плоскости граней В1С1СВ и A1D1DA пересечены плоскостью A1C1CA, линии пересечения параллельны, АА1 || СС1. АА1 = СС1 (по свойству: отрезки параллельных прямых, заключенных между параллельными плоскостями, равны). АА1 || СС1 и АА1 = CC1 (по признаку параллелограмма), АА1С1С - параллелограмм.
Задача 81
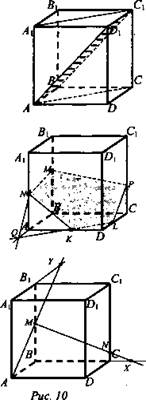
а) Пусть MN не параллельна ВС, тогда MN пересечет плоскость ABC.
Построение: продолжим отрезки ВС и MN до пересечения в точке х. Тогда точка х искомая.
б) AM не параллельна А1В1, AM пересечет А1В1, А1В1С плоскости А1B1C1.
Построение: Продолжим отрезки А1В1 и AM до пересечения в точке Y. Точка Y - искомая (рис. 10).
Задача 87 а)
Построение:
1. Допустим, что MN не параллельна АВ.
2. Продолжим MN и АВ до пересечения их в точке О.
3. ОК ⊂ ABC (так как О принадлежит плоскости ABC и К принадлежит плоскости ABC).
4. Соединим точки К и N.
5. Плоскости ONK и ОАК (то есть плоскость ABC) пересекаются по прямой ОК.
6. Поэтому продолжим ОК до пересечения с DC в точке L. Соединим точки К и L, ведь они лежат в одной плоскости.
7. Противоположные грани АА1В1В и DD1C1C секущая плоскость пересечет по параллельным прямым (по теореме: через две пересекающие прямые проходит плоскость, и притом только одна), поэтому в плоскости DD1C1C проведем LP || NM.
8. Соединим точки Р и М.
9. MNKLP - искомое сечение.
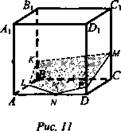
Задача 87 б)
Построение:
1. Соединим точки К и М.
2. Точка N принадлежит грани AA1D1D и секущей плоскости.
3. Секущая плоскость, проходящая через точку N, пересечет параллельные грани AA1D1D и ВВ1С1С по параллельным прямым; поэтому в плоскости AA1D1D проводим NP || КМ.
4. Проводим РМ.
5. Секущая плоскость проходит через точку К и пересекает противоположные грани АА1В1В и DD1C1C по параллельным прямым; поэтому в плоскости грани АА1В1В проводим KL || МР.
6. Соединим L и М.
7. KLNPM - искомое сечение (рис. 11).
VI. Подведение итого.
Оценки.