Поурочные разработки по геометрии 10 класс
Контрольная работа № 1 - ТЕТРАЭДР. ПАРАЛЛЕЛЕПИПЕД - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) проверка знаний, умений и навыков при решении задач;
2) умение объяснять смысл решения задач.
Ответы:
I уровень
Вариант I
1. Дано: 
(рис. 1).
Найти: А1В1.
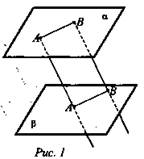
Решение: α || β; АА1 || ВВ1 по свойству отрезков ⇒ АА1 = ВВ1 ⇒ АВВ1А1 - параллелограмм ⇒ АВ = А1В1 = 5 см. (Ответ: A1B1 = 5 см.)
2. Дано: a ⊂ α; а || β (рис. 2).
Верно ли: α || β?
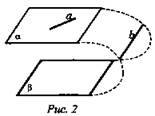
Решение:
Пусть 
, тогда 
(возможно) ⇒ α ∩ β по прямой ⇒ α || β. (Ответ: не верно.)
3. Дано: а 
(рис. 3).
Найти: МА2, МВ2.
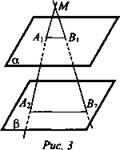
Решение:
1) а 
по свойству параллельных плоскостей A1B1 || А2В2;
2) 
Пусть А1А2 = х; 
МВ2 = 6 + 9 = 15 см. (Ответ: МА2 = 10 см, МВ2 = 15 см.)
Вариант II
1. Дано: 
(рис. 4).
Найти: АВ.
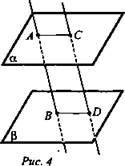
Решение: 
по свойству параллельных плоскостей АВ = CD. АВ = 3 см. (Ответ: АВ = 3 см.)
2. Дано: 
(рис. 5).
Верно ли: α || β?
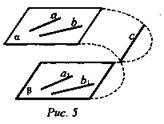
Решение: Пусть 
(может) ⇒ по признаку параллельности прямой и плоскости ⇒ α || β (не верно). (Ответ: не верно.)
3. Дано: 
АВ = b, ВС = а (рис. 6).
Найти: РA1B1C1.
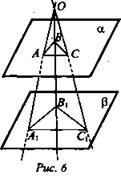
Решение:
1) α || β.
2) 
по свойству параллельности АС || А1С1.
3) 
4) Аналогично: 
5) 
6) По свойству периметров подобных многоугольников: 
(Ответ: 
)
Вариант I
II уровень
1. Дано: DABC - треугольная пирамида; К ⊂ DN (рис. 7а).
Построить: сечение.
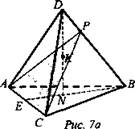
Построение:
1) ЕК.
2) ЕК ∩ DB = Р.
3) PC.
4) РА.
5) АРС - искомое сечение.
2. Дано: ABCDA1B1C1D1 - куб. АА1 = 2 см (рис. 9).
Найти: АО.
Решение:
1) 
AO ⊥ (B1BD); АО - расстояние между скрещивающимися прямыми АВ и B1D.
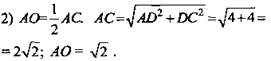
3. Дано: α || α1; β || β1 (рис. 10).
Доказать: m || m1; n || n1.
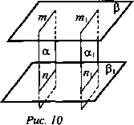
Доказательство:
1) 
по свойству m || n;
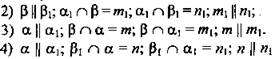, что и требовалось доказать.
Вариант II
1. Дано: MABCD - четырехугольная пирамида; N ∈ МС (рис. 8 а).
Построить: сечение.
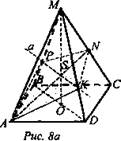
Построение:
1) AN.
2) AN ∩ МО = S.
3) α || BD, S ∈ α.
4) 
5) AP, PN, NK, AK.
6) APNK - искомое сечение.
2. Дано: ABCDA1B1C1D1 - прямой параллелепипед; ABCD - основание (ромб); ∠BAD = 30°; АВ = 18, ВВ1 = 12 (рис. 11).
Найти: SAB1C1D.
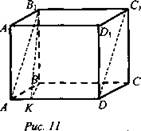
Решение:
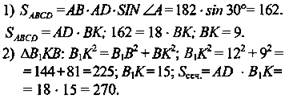
(Ответ: SAB1C1D = 270.)
3. Дано: α || β; AB || CD (рис. 12).
Найти: Каково взаимное расположение прямых АС и BD.
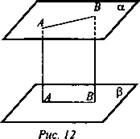
Решение: Пусть AC || BD, тогда по свойству параллельных прямых АС = BD ⇒ ABCD - параллелограмм ⇒ АВ || CD, что противоречит условию ⇒ АС || BD. (Ответ: AC || BD.)
III уровень
Вариант I
1. Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед; М ∈ АВ, N ∈ AD (рис. 13 а).
Построить: сечение.
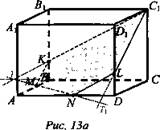
Построение:
1) MN.
2) MN ∩ ВС = Т.
3) ТС1 ∩ BB1 = К.
4) МК, КС1.
5) MN ∩ CD = T1.
6) T1C1 ∩ DB1 = L.
7) NL.
8) LC1.
9) MKC1LN - искомое сечение.
2. Дано: α || β; АВ - перпендикуляр; АВ = 3 м; CD - наклонная, CD = 5 м; АС = BD = 4 м. (рис. 15).
Найти: PQ.
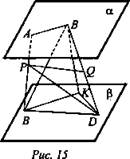
Решение:
1) ΔРАС - прямоугольный. Так как 
2) ΔPBD - прямоугольный. Так как 
3) ΔDPC - равнобедренный ⇒ PQ - медиана и высота;
4) ΔPQC - прямоугольный; 
(Ответ: 
)
Вариант II
1. Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед; 
(рис. 14 а).
Построить: сечение.
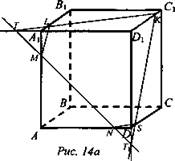
Построение:
1) MN.
2) MN ∩ A1D1 = Т.
3) TK ∩ A1D1 = L.
4) LK, LM.
5) MN ∩ DD1 = Т1.
6) T1K ∩ DC = S.
7) C1S, NS.
8). M ⊥ KSN - искомое сечение.
2. Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед; Р - середина отрезка В1С; N - середина отрезка A1B1; AD = а, АВ = b, АА1 = С (рис. 16).
Найти: D1P, CN.
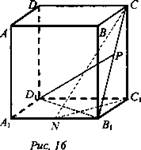
Решение:
1) ΔВ1С1С-прямоугольный: СВ12 = a2 + c2.
2) ΔD1DC - прямоугольный: D1С = с2 + b2.
3) ΔD1B1С1 - прямоугольный: D1B12 = a2 + b2.
4) ΔCD1B1: D1P - медиана: 
5. ΔNB1C1 - прямоугольный: 
.
6. ΔNCC1 - прямоугольный: 
(Ответ: 
)