Поурочные разработки по геометрии 10 класс
Зачет № 1 - ТЕТРАЭДР. ПАРАЛЛЕЛЕПИПЕД - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) проверка теоретических знаний по теме;
2) выявление уровня усвоения основных геометрических понятий и умение применять их на практике.
Ход урока
I. Организационный момент
Сообщить тему урока и сформулировать цели урока.
II. Устный опрос (задания со «*» предлагаются более сильным учащимся)
1. Какие плоскости называются параллельными? Привести наглядные примеры (определение).
2. Как читается признак параллельности плоскостей? (теорема)
3. Как используют этот признак на практике? (Ответ: а) чтобы распилить брус, так чтобы плоскости распилов были параллельны, на двух смежных гранях бруса прочерчивают а1 || а и b1 || b и по ним направляют движение пилы; б) чтобы получить горизонтальную плоскость, например, для фундамента здания, межэтажного перекрытия, футбольного поля и т.д. устанавливают по уровню, что этой плоскости принадлежат две пересекающиеся горизонтальные прямые а и b.)
4. Найдите ошибку в таком признаке: Две плоскости параллельны, если две прямые одной плоскости параллельны двум прямым другой плоскости. (Ответ: нет точки пересечения, следовательно, прямые могут быть параллельными линиям пересечения плоскостей.)
5. Что можно сказать о противоположных гранях прямоугольного параллелепипеда? (Ответ: параллельны, так как соответствующие пересекающиеся ребра одной грани параллельны пересекающимся ребрам другой грани.)
*6. Дано: α || β; b ∈ β (рис. 1).
Доказать: b || α.
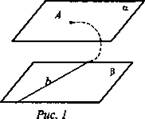
Доказательство:
1) Пусть ![]()
2) ![]() по прямой b, что противоречит условию. Следовательно, b || α.
по прямой b, что противоречит условию. Следовательно, b || α.
7. Прямые а и b скрещивающиеся, провести через прямые а и b параллельные плоскости (объяснить ответ).
Дано: а, b - скрещивающиеся (рис. 2).
Построить: α || α1.
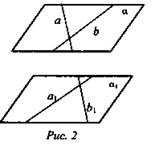
Построение.
1) ![]()
2) ![]()
*8. В треугольной пирамиде надо провести сечение через точку основания, параллельно боковой грани. Как определить положение секущей плоскости? (рис. 3).

Построение:
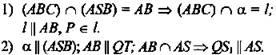
3) (QS1T) - искомое сечение.
9. Две стороны треугольника параллельны
плоскости. Что можно сказать о третьей стороне? (Ответ: параллельна плоскости.)
* 10. Плоскость, проведенная через середины ребер AD, DC и A1D, куба ABCDA1B1C1D1 параллельна диагональному сечению АА1С1С (рис. 4).
Докажите: PQ - средняя линия ΔADC ⇒ PQ || АС; РТ - средняя линия ΔA1D1D ⇒ РТ || АА1 = (РTQ) || (AA1C1).
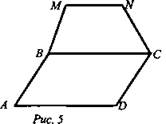
11. Ромб ABCD и трапеция BMNC не лежат в одной плоскости (рис. 5). Как расположены прямые MN и AD? (Ответ: параллельны.)
*12. Могут ли пересекаться плоскости (рис. 6), параллельные одной и той же прямой? (Ответ: Да. Прямая параллельна линии пересечения плоскостей..
1) с || α ⇒ а || с;
2) с || β ⇒ а || с ⇒ а - линия пересечения α и β.
