Поурочные разработки по геометрии 10 класс
Решение задач на перпендикулярность прямой и плоскости - урок 3 - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) совершенствовать навыки решения задач;
2) проверить теоретические знания, умение решать задачи и навыки учащихся по теме «Перпендикулярность прямой и плоскости».
Ход урока
I. Организационный момент
Сообщить тему урока, сформулировать цели урок.
II. Актуализация знаний учащихся
1. Разобрать задачи из домашнего задания, с которыми не справились большинство учащихся.
2. Решение задач на готовых чертежах (для учащихся, справившихся с домашним заданием).
Решение проводится с последующей проверкой и обсуждением решения для учащихся всего класса.
Прямая а перпендикулярна плоскости ABC (рис. 1, 2, 3, 4).
1. Рис. 1. ∠ACB = 90°, АС = 4, MD = 3. Найти: МС.
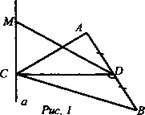
2. Рис. 2. ΔАВС - равносторонний, АВ = 2√3, MD = 4. Найти: МС.
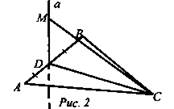
3. Рис. 3. Найти: MB.
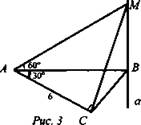
4. Рис. 4. ABCD - прямоугольник, MD = 8. Найти: АВ и AD.
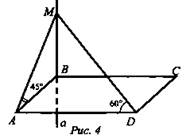
Решения к задачам на готовых чертежах
№ 1
Решение:
1) Так как CD - медиана и высота в ΔАВС, то ΔАВС - равнобедренный (по признаку) ⇒ АС = ВС = 4.
2) ΔАВС - прямоугольный (∠ACB = 90°). По теореме Пифагора: АВ2 = АС2 + ВС2 = 42 + 42 = 32, ![]() (по свойству медианы, проведенной к гипотенузе).
(по свойству медианы, проведенной к гипотенузе).
3) Так как ![]() ΔMCD - прямоугольный. По теореме Пифагора:
ΔMCD - прямоугольный. По теореме Пифагора: ![]()
![]() (Ответ: 1.)
(Ответ: 1.)
№ 2
Решение:
1) Так как CD - медиана равностороннего треугольника, то ![]()
2) Так как ![]()
3) ΔMDC - прямоугольный. По теореме Пифагора: МС2 = MD2 + DC2, МС2 = 42 + 32 = 25, МС = 5. (Ответ: 5.)
№ 3
Решение:
1) 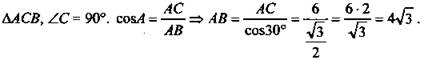
2) ![]() ΔАВМ - прямоугольный;
ΔАВМ - прямоугольный; ![]() (Ответ: 12.)
(Ответ: 12.)
№ 4
Решение:
1) Так как 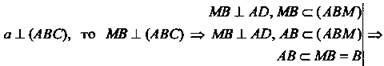
![]()
2) ΔMAD - прямоугольный: ![]()
![]()
3) ![]() ΔABM - прямоугольный:
ΔABM - прямоугольный: ![]() (Ответ: 2√6.)
(Ответ: 2√6.)
III. Самостоятельная работа (см. приложение)
Решение задач самостоятельной работы
I уровень
Вариант I
№ 1. Дано: α, АВ - отрезок, ![]()
![]()
![]() (рис. 5).
(рис. 5).
Найти: АВ.
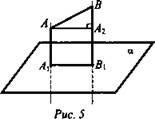
Решение:
1) Так как ![]() и существует плоскость β:
и существует плоскость β: ![]()
![]() Тогда ABB1A1 - трапеция с основаниями АА1 и ВВ1.
Тогда ABB1A1 - трапеция с основаниями АА1 и ВВ1.
2) Пусть AA2 - высота ![]()
![]() тогда АА2В1А1 - прямоугольник;
тогда АА2В1А1 - прямоугольник; ![]()
![]() (по свойству сторон прямоугольника);
(по свойству сторон прямоугольника); ![]() то
то ![]()
3) Так как АА2 - высота, то ![]()
![]() ΔАА2В - прямоугольный, по теореме Пифагора
ΔАА2В - прямоугольный, по теореме Пифагора ![]()
![]()
![]()
№ 2. Дано: ABCD - прямоугольник; ![]()
![]() (рис. 6).
(рис. 6).
Найти: В1В.
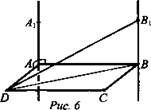
Решение:
1) 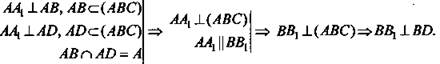
2) ΔABD, ∠A = 90°. По теореме Пифагора: BD2 = AB2 + AD2. ![]()
3) Так как BD ⊥ ВВ1, то ∠B1BD = 90°. ΔB1BD - прямоугольный. По теореме Пифагора: ![]()
![]() (Ответ: 15 см.)
(Ответ: 15 см.)
Вариант II
№ 1. Дано: α, АВ - отрезок, АВ ![]()
![]()
Найти: А1В1.
Решение:
1)-2) см. решение задачи № 1 (I вариант); ![]()
![]()
3) ∠AA2B = 90°, ΔАА2В - прямоугольный. По теореме Пифагора: ![]()
![]() Значит, А1В = 12 см. (Ответ: 12 см.)
Значит, А1В = 12 см. (Ответ: 12 см.)
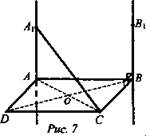
№ 2. Дано: ABCD - ромб; ![]()
![]() (рис. 7).
(рис. 7).
Найти: АА1.
Решение:
1) 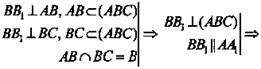
![]()
2) АС ⊥ BD и АО = ОС, ВО = OD (по свойству диагоналей ромба). В ΔAОВ: ∠AОВ = 90°, ![]() По теореме Пифагора:
По теореме Пифагора: ![]()
![]()
3) ![]() ΔA1АС - прямоугольный, по теореме Пифагора
ΔA1АС - прямоугольный, по теореме Пифагора ![]() (Ответ: 5 см.)
(Ответ: 5 см.)
II уровень
Вариант I
№ 1. Дано: ![]()
![]()
![]() (рис. 8).
(рис. 8).
Найти: АВ.
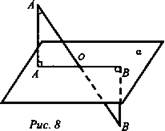
Решение:
1) ![]()
2) Так как ![]()
![]() Тогда существует плоскость β:
Тогда существует плоскость β: ![]()
3) ΔАА1О и ΔВВ1О - прямоугольные, ![]() (по свойству накрест лежащих углов, образованных параллельными прямыми АА1 и ВВ1 и секущей АВ) ΔАА1О ~ ΔBB1O (по равенству острых углов) ⇒
(по свойству накрест лежащих углов, образованных параллельными прямыми АА1 и ВВ1 и секущей АВ) ΔАА1О ~ ΔBB1O (по равенству острых углов) ⇒ ![]() (по определению подобных треугольников);
(по определению подобных треугольников); ![]()
4) В ![]() так как
так как ![]() то
то ![]() Тогда
Тогда ![]() (Ответ: 24 см.)
(Ответ: 24 см.)
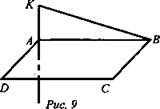
№ 2. Дано: ABCD - прямоугольник; КА прямая КА ⊥ (ABC) (рис. 9).
Доказать: КВ ⊥ ВС.
Доказательство:
1) ![]() (по определению прямой, перпендикулярной плоскости).
(по определению прямой, перпендикулярной плоскости).
2) Так как ABCD - прямоугольник, то ![]()
3) 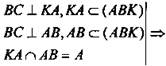 ВС ⊥ (АВК) (по признаку перпендикулярности прямой и плоскости).
ВС ⊥ (АВК) (по признаку перпендикулярности прямой и плоскости).
4) ![]() ВС ⊥ КВ (по определению прямой, перпендикулярной плоскости).
ВС ⊥ КВ (по определению прямой, перпендикулярной плоскости).
Вариант II
№ 1. Дано: α, АВ - отрезок, АВ ![]()
![]() (рис. 8).
(рис. 8).
Найти: АВ.
Решение:
1)-3) см. решение задачи № 1 (вариант I); ![]()
![]() Так как ∠A = ∠B = 45, то ΔАА1О и ΔВВ1О - равнобедренные прямоугольные треугольники
Так как ∠A = ∠B = 45, то ΔАА1О и ΔВВ1О - равнобедренные прямоугольные треугольники ![]()
4) ![]()
(Ответ: 8 см.)
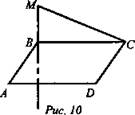
№ 2. Дано: ABCD - квадрат; MB - прямая; MB ⊥ (ABC) (рис. 10).
Доказать: МС ⊥ CD.
Доказательство:
1) ![]()
2) Так как ABCD - квадрат, то ![]()
![]()
3) 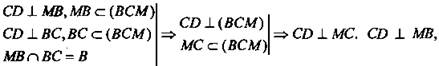
![]()
III уровень
Вариант I
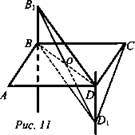
№ 1. Дано: ABCD - прямоугольник; ![]()
![]()
![]() (рис. 11).
(рис. 11).
Доказать: ![]()
Найти: B1D1.
Решение:
1) ![]() (пo теореме, устанавливающей связь между параллельностью прямых и их перпендикулярностью к плоскости); АВ || CD (по свойству сторон прямоугольника);
(пo теореме, устанавливающей связь между параллельностью прямых и их перпендикулярностью к плоскости); АВ || CD (по свойству сторон прямоугольника); ![]()
![]() Следовательно,
Следовательно, ![]() (пo признаку).
(пo признаку).
2) ![]() - параллелограмм (по признаку)
- параллелограмм (по признаку)
![]() (по свойству диагоналей параллелограмма).
(по свойству диагоналей параллелограмма).
3) ΔBAD, ∠A = 90°. По теореме Пифагора: BD2 = AB2 + AD2 (AD = ВС); ![]()
4) ![]()
5) ΔD1DO - прямоугольный, по теореме Пифагора: D1О2 = D1D2 + DO2. ![]() (Ответ: 26 см.)
(Ответ: 26 см.)
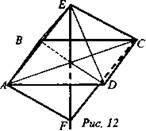
№ 2. Дано: ABCD и AECF - квадраты; BD ⊥ EF (рис. 12).
Доказать: EF ⊥ (ABC).
Найти: ∠(АС; ED).
Решение:
1) АС ⊥ EF (по свойству диагоналей квадрата); BD ⊥ EF (по условию). ![]() и
и ![]() по признаку.
по признаку.
2) 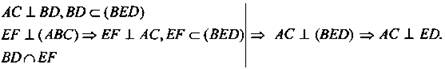 Значит, ∠(AC, ED) = 90°.
Значит, ∠(AC, ED) = 90°.
(Ответ: 90°.)
Вариант II
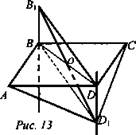
№ 1. Дано: ABCD - прямоугольник; ![]()
![]()
![]() (рис. 13).
(рис. 13).
Найти: SABCD.
Доказать: ![]()
Решение:
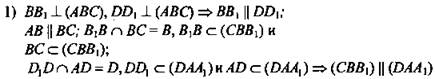 (no признаку).
(no признаку).
2) ![]() - параллелограмм,
- параллелограмм, ![]()
![]()
3) ![]() - прямоугольный, по теореме Пифагора:
- прямоугольный, по теореме Пифагора: ![]()
![]()
4) ![]() По теореме Пифагора:
По теореме Пифагора:
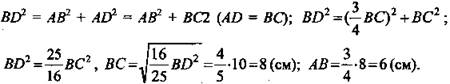
5) ![]() (Ответ: 48 см2.)
(Ответ: 48 см2.)
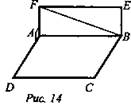
№ 2. Дано: ABCD и ABEF - квадраты; AD ⊥ AF (рис. 14).
Доказать: ВС ⊥ (AEF).
Найти: ∠(AD; BF).
Решение:
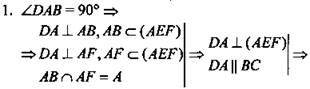 ВС ⊥ (AEF) (по теореме, обратной к теореме, устанавливающей зависимость между параллельностью прямых и их перпендикулярностью к плоскости).
ВС ⊥ (AEF) (по теореме, обратной к теореме, устанавливающей зависимость между параллельностью прямых и их перпендикулярностью к плоскости).
2) Так как ![]() (по определению прямой перпендикулярной плоскости). Значит, ∠(AD, BF) = 90°.
(по определению прямой перпендикулярной плоскости). Значит, ∠(AD, BF) = 90°.
IV. Проведение итогов
Домашнее задани.
Решить задачи
I уровень - задачи II уровня (или III уровня, по усмотрению учителя) самостоятельной работы;
II уровень - задачи III уровня (или другой вариант) самостоятельной работы.