Расстояние от точки до плоскости. Теорема о трех перпендикулярах - ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ. УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

Цели урока:

1) ввести понятие расстояния от точки до плоскости;

2) доказать теорему о трех перпендикулярах. Показать применение этой теоремы при решении задач.

Ход урока

I. Организационный момент

II. Актуализация опорных знаний

1. Теоретический опрос (фронтальная работа с классом).

1.1. Угол между прямыми равен 90°. Как называются такие прямые? (Перпендикулярные.)

1.2. Верно ли утверждение: «Прямая называется перпендикулярной плоскости, если она перпендикулярна некоторой прямой, лежащей в этой плоскости?» (Да.)

1.3. Продолжите предложение: «Прямая перпендикулярна плоскости, если она...» (перпендикулярна к двум пересекающимся прямым, лежащим в этой плоскости).

1.4. Что можно сказать о двух (3-х, 4-х) прямых, перпендикулярных к одной плоскости? (Они параллельны.)

1.5. Две прямые, перпендикулярные третьей прямой, ... (параллельны.)

1.6. Как определяется расстояние от точки до прямой на плоскости?

Возможный ответ: как кратчайшее расстояние от точки до прямой, как длина перпендикуляра, проведенного из точки к данной прямой. Верно.

1.7. (Рис. 1).

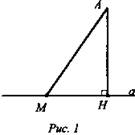
Вспомним, как называются отрезки AM - ? АН - ? Точка М? Точка – H?

1.8. А как же определить расстояние от точки до плоскости?

III. Изучение нового материала

1. Вводится понятие перпендикуляра к плоскости, наклонной, проекции наклонной на плоскость.

Рассмотрим плоскость а и точку А ∉ α (рис. 2).

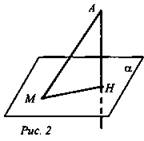
Учитель вычерчивает рис. 51 учебника на доске, учащиеся в тетрадях.

1) Точку А, прямую а ⊥ α, а ∩ α = Н, АН - перпендикуляр, Н - основание перпендикуляра;

2) Отметим в плоскости α произвольную точку М, отличную от Н. AM - наклонная, проведенная из А к плоскости α, НМ - проекция на плоскость α.

3) Докажите, что АН < AM; - чему равен ∠MHA? ∠MHA = 90°, ⇒ ΔAHМ прямоугольный, АН - катет, AM - гипотенуза, поэтому АН < AM.

Вывод. Перпендикуляр, проведенный из данной точки к плоскости, меньше любой наклонной, проведенной из той же точки к этой плоскости.

4) Рассмотрите рис. 52, стр. 41 учебника, 2 абзац сверху прочитать.

2. Вводится понятие расстояния от точки А до плоскости, расстояние между параллельными плоскостями, расстояние между прямой и параллельной ей плоскостью, расстояние между скрещивающимися прямыми.

Что называется расстоянием от точки А до плоскости α?

Расстоянием от точки А до плоскости а называется длина перпендикуляра, проведенного из точки А к плоскости а (рис. 3).

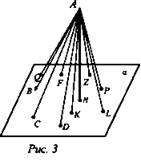
- Назовите наклонные по рис. 3.

- Назовите перпендикуляр.

Вычертить чертежи 4-7 в тетрадях. Учитель рассказывает по чертежам (или по готовой таблице).

Если α || β, то все точки плоскости α равноудалены от другой плоскости. Пусть проведем тогда

Расстоянием между параллельными плоскостями называется расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости.

Если а || α, то все точки прямой равноудалены от этой плоскости (рис. 4).

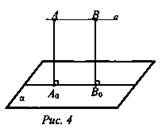
Задача 144 (стр. 45 - дома)

Расстоянием между прямой и плоскостью называется расстояние от произвольной точки прямой до плоскости.

Расстоянием между скрещивающимися прямыми называется расстояние между одной из из них и плоскостью (рис. 5), проходящей через другую прямую, параллельно первой прямой. Если а и b скрещиваются, пусть М ∈ b. Проведем а1 || а. Через

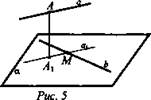
Из произвольной

Записываем в тетрадях и на доске вывод (рис. 6): - скрещивающиеся.

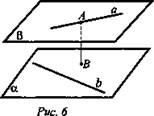
Длина отрезка АВ - расстояние между:

1) плоскостями α и β;

2) прямой а и плоскостью α;

3) прямыми а и b.

3. Докажем теорему о трех перпендикулярах.

Теорема:

Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.

Вопрос: Что же дано в этой теореме?

Дано: АН ⊥ α, AM - наклонная к плоскости α (рис. 7). НМ - проекция наклонной, а ∈ α, а ⊥ НМ.

Доказать: а ⊥ AM.

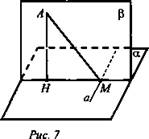
Доказательство: АН ⊥ а, так как АН ⊥ α ⇒ а ⊥ β по признаку перпендикулярности прямой и плоскости, ⇒ а ⊥ AM по определению перпендикулярности прямой и плоскости.

Вопрос: О каких же трех перпендикулярах идет речь в теореме?

Три перпендикуляра: а, НМ, AM.

Обратная теорема:

Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.

Дано: АН ⊥ α, AM - наклонная к плоскости α, НМ - проекция наклонной, а ∈ α, a ⊥ AM.

Доказать: а ⊥ НМ.

Доказательство', задача 153, стр. 45, дома разобрать самостоятельно.

поэтому a ⊥ НМ.

IV. Применение знаний в стандартной ситуации

Задача № 139

Из некоторой точки проведены две наклонные.

Докажите, что: а) если наклонные равны, то равны и их проекции; б) если проекции наклонных равны, то равны наклонные; в) если наклонные не равны, то большая наклонная имеет большую проекцию.

Выполним чертеж, решим задачу устно.

Дано: АН ⊥ α, АВ и АС наклонные; а) АВ = АС; б) ВН = НС; в) АВ1 >АС (рис. 8).

Доказать: а) ВН = НС; б) АВ = АС; в) В1Н > СН.

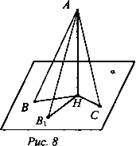
Доказательство:

Рассмотрим ΔАВН и ΔАСН: АН - общий катет;

а) АВ = АС гипотенузы ⇒ ΔАВН = ΔАСН по гипотенузе и катету, значит, ВН = НС;

б) аналогично ΔАВН = ΔАСН по двум катетам (I пр.) ⇒ АВ = АС;

в) из неравенства треугольника.

3) АВ1 - АС > 0, так как АВ1 > АС1; А1В - АН > АС – АН; А1В > АС.

Задача 145

Через вершину А прямоугольного треугольника ABC с прямым углом С проведена прямая AD, перпендикулярная к плоскости треугольника.

а) Докажите, что ΔCBD прямоугольный.

б) Найдите BD, если ВС = a, DC = b.

Дано: ΔАВС, ∠C = 90°, AD ⊥ плоскости; ΔАВС, ВС = a, DC = b (рис. 9).

а) Доказать, что ACBD - прямоугольный.

б) Найти: BD.

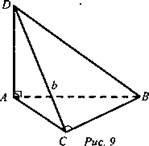
Решение:

а) АС проекция наклонной DC на плоскости ΔАВС. ВС ⊥ АС по условию ⇒ ВС ⊥ DC по теореме о трех перпендикулярах, значит, ΔCBD - прямоугольный;

б) Из ΔBCD ∠С = 90° по теореме Пифагора. (Ответ: )

V. Подведение итогов

Домашнее задание

Пункты 19, 20, разобрать самостоятельно замечания (второе, № 144), обратная теорема № 153 (144 и 153 решены), решить задачи № 143, 140. Замечание 2 можно предложить доказать не как в № 144.

II способ

Пусть (чертеж, стр. 3, рис. 5.).

Проведем Тогда АА1 || ВВ1.

Докажем, что АА1 = ВВ1.

Плоскость, проходящая через параллельные прямые АА1 и ВВ1, пересекается с α по прямой A1B1 и содержит прямую АВ. Ясно, что АВ || А1В1 (если бы что противоречит условию). Итак, - параллелограмм, ⇒ АА1 = ВВ1.

№ 143

Расстояние от точки М до каждой из вершин правильного ΔABC равно 4 см (рис. 10).

Найдите расстояние от токи М до плоскости ABC, если АВ = 6 см.

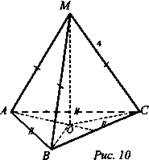
Решение: По условию МА = MB = МС = 4 см. Пусть МО ⊥ ABC, тогда ОА = ОВ = ОС, как проекции равных наклонных. Значит, О - центр окружности, описанной около ΔABC, а ОА - радиус этой окружности. а3 = R√3, где АВ = а3, R = АО поэтому Из ΔМАО: (Ответ: 2 см.)

№ 140

Из точки А, не принадлежащей плоскости α, проведены две наклонные АВ и АС равные и перпендикуляр АО. Известно, что ∠AOB = ∠ВАС = 60°, АО = 1,5 см. Найдите расстояние между основаниями наклонных.

Дано: наклонные, (рис. 12).

Найти: ВС.

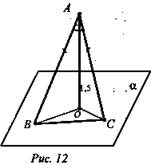
Решение:

против ∠30° лежит катет

3) ΔABC, ∠BAC = 60°, АВ = АС по условию, АС = 3 см. ΔАВС равнобедренный ΔABC - равносторонний. ВС = АВ = AС = 3 см. (Ответ: 3 см.)