Поурочные разработки по геометрии 10 класс
Угол между прямой и плоскостью (повторение) - ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ. УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) ввести понятие прямоугольной проекции фигуры;
2) дать определение угла между прямой и плоскостью;
3) научить решать задачи на нахождение угла между прямой и плоскостью.
Ход урока
I. Проверка домашнего задания (10 мин)
Вспомнить с учащимися теорему о 3-х перпендикулярах.
№ 204. Дано: ОМ ⊥ (ABC), ОМ проходим через центр правильного ΔАВС; ОМ = a; ∠MCO = φ (рис. 1).
Найти: ОЕ; ME; SΔABC.
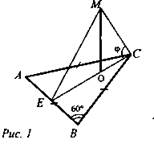
Решение:
а) ОА = ОВ = ОС = R - радиус описанной окружности около ΔАВС, ![]()
б) ΔАВС - правильный: СЕ ⊥ АВ, ОЕ = r, r — радиус вписанной окружности; ME ⊥ АВ (по теореме о 3-х перпендикулярах); ME - расстояние от точки М до АВ; ![]()
![]()
в) Из ΔМОЕ: ![]()
г) Длина окружности ![]()
д) ![]()
е) ![]()
![]() (Ответ:
(Ответ: ![]() )
)
№ 206. Дано: АВ = 17 см; АС = 15 см; ВС = 8 см, АМ ⊥ (ABC), ∠А — меньший, АМ = 20 см (рис. 2).
Найти: ME.
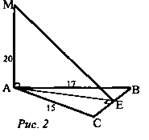
Решение:
1) В ΔАВС против меньшей стороны лежит меньший угол (по теореме синусов). Проведем АЕ ⊥ ВС, АЕ ⊥ ME. По теореме о 3-х перпендикулярах ME ⊥ ВС.
2) По формуле Герона:

По теореме Пифагора: ![]() (Ответ: 25 см.)
(Ответ: 25 см.)
II. Объяснение материала (8 мин)
Проекция произвольной фигуры - основание перпендикуляра, проведенного из этой точки к плоскости, если точка не лежит в плоскости, и сама точка, если она лежит в плоскости (рис. 3).
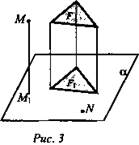
М1 - проекция точки М на плоскость α; N - проекция самой точки N; (N ∈ α); F - фигура в пространстве; F1 - проекция фигуры F на данную плоскость.
Определение:
Угол между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость (рис. 4).
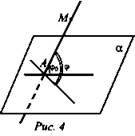
φ0 - угол между прямой AM и плоскостью α является наименьшим из всех углов φ, которые данная прямая образует с прямыми, проведенными в плоскости α через точку А.
1) Если прямая перпендикулярна к плоскости, то ее проекцией на эту плоскость является точка пересечения этой прямой с плоскостью. Угол между прямой и плоскостью считается равным 90°.
2) Если прямая параллельна плоскости, то ее проекцией на плоскость является прямая, параллельная данной.
Понятие угла между прямой и плоскостью не вводим.
Угол между параллельными прямой и плоскостью считать равным 0°.
III. Закрепление материала (14 мин)
1. Учащиеся оформляют в тетрадях решение задачи № 162 из учебника и решение задачи на доске (9 мин.).
Задача
Найдите угол между скрещивающимися прямыми АВ и PQ, если каждая из точек Р и Q равноудалена от концов отрезка АВ.
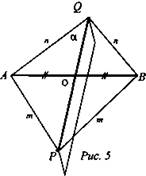
Решение: РА = РВ = m; QA = QB = n. Точки Р и Q лежат в плоскости α, проходящей через середину АВ и АВ ⊥ α. PQ ⊂ α и PQ ⊥ АВ, то есть искомый угол 90°. (Ответ: 90°.)
2. Один из учеников у доски решает задачу (5 мин.)
№ 163 (учащиеся решают в тетрадях)
Дано: АМ = d; ∠AMB = φ; а) 45°; б) 60°; в) 30° (рис. 6).
Найти: MB.
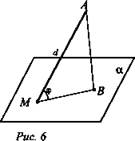
Решение:
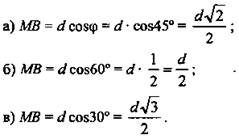
(Ответ: ![]() )
)
IV. Самостоятельная работа (7 мин.
Вариант I. Задача № 208.
Вариант II. Задача № 209.
№ 208 (рис. 7)
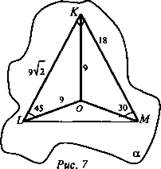
1) ΔLOK и ΔМОК - прямоугольные (по условию КО ⊥ α).
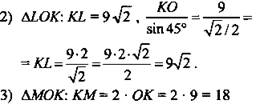 (ОK лежит против угла в 30°).
(ОK лежит против угла в 30°).
4) ΔKLM- прямоугольный, ![]() (Ответ: 9√6 см.)
(Ответ: 9√6 см.)
Домашнее задание
П. 21, задачи № 164 и № 165. п. 20.
№ 209 (рис. 8)
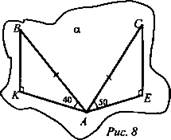
1) Проведем СЕ ⊥ α, ВК ⊥ α.
Пусть АВ = АС = а, тогда В К = a sin 40°, СЕ = a sin 50°.
2) Так как sin 50° > sin 40°, то СЕ > ВК расстояние от точки С больше. (Ответ: расстояние от точки С до плоскости больше.)