Поурочные разработки по геометрии 10 класс
Двугранный угол - ДВУГРАННЫЙ УГОЛ. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) ввести понятие двугранного угла и его линейного угла;
2) рассмотреть задачи на применение этих понятий;
3) сформировать конструктивный навык нахождения угла между плоскостями.
Ход урока
I. Организационный момент
Сообщить тему урока, сформировать цели урока.
II. Актуализация знаний учащихся
1. Сообщить итоги самостоятельной работы.
Анализ распространенных ошибок.
2. Проверка домашнего задания.
3. Подготовка к изучению нового материала.
- Что называется углом на плоскость?
- Что называется углом между прямыми в пространстве?
- Что называется углом между прямой и плоскостью?
III. Изучение нового материала
1. Понятие двугранного угла (рис. 1 а, б).
а) прямая а разделяет плоскость на две полуплоскости;
б) двугранный угол.
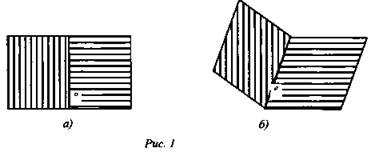
Вывод:
Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости.
Полуплоскости - грани, прямая а - ребро двугранного угла.
- Какие предметы в обыденной жизни имеют форму двугранного угла?
(Полураскрытая папка, стена комнаты совместно с полом, двускатные крыши зданий и т.д.)
2. Пусть О ∈ а, АО ⊥ а, ВО ⊥ a, ∠AOB - линейный угол двугранного угла (рис. 2, 3).
3. Все линейные углы двугранного угла равны.
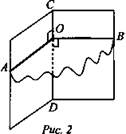
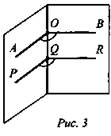
Докажем это.
Рассмотрим два линейных угла АОВ и PQK. Лучи ОА и QP лежат в одной грани и перпендикулярны OQ, значит, они сонаправлены. Аналогично лучи ОВ и QR сонаправлены. Значит, ∠AOB = ∠PQR (как углы с сонаправленными сторонами).
4. Градусной мерой двугранного угла называется градусная мера его линейного угла.
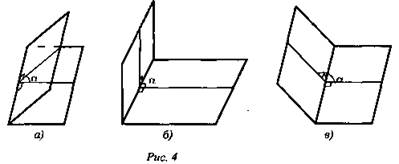
а) острый (α < 90°); б) прямой (α = 90°); в) тупой (90° < α < 180°).
5. Обозначение двухранного угла.
Двугранный угол с ребром АВ, на разных гранях которого отмечены точки С и D, называется двугранным углом CABD.
IV. Закрепление изученного материал.
1. Сделайте чертежи к задачам
№ 1
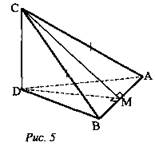
Дано: ΔABC, АС = ВС, АВ лежит в плоскости α, CD ⊥ α, С ∉ α (рис. 5).
Построить линейный угол двугранного угла CABD. CM ⊥ AB, DC ⊥ АВ. ∠CMD - искомый.
№ 2
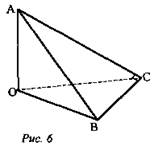
Дано: ΔABC, ∠C = 90°, ВС лежит плоскости α, АО ⊥ α, A ∈ α (рис. 6).
Построить АВСО. AB ⊥ BC, АО ⊥ ВС, значит, ОС ⊥ ВС. ∠ACO - искомый.
№ 3
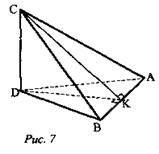
Дано: ΔABC, ∠С = 90°, АВ лежит в плоскости α, CD ⊥ α, С ∉ α (рис. 7).
Построить DABC. CK ⊥ AB, DC ⊥ АВ, DK ⊥ АВ, значит, ∠DKC - искомый.
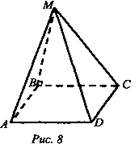
Дано: ABCD - квадрат, MB ⊥ ABC (рис. 8).
Построить:
а) (MDC; АВС); б) MADB; a) ∠MCB - искомый; б) ∠MAD - искомый.
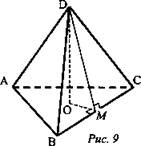
Дано: DABC - тетраэдр, DO ⊥ ABC (рис. 9).
Построить: ABCD
DM ⊥ ВС, DO ⊥ ВС, значит, ОМ ⊥ ВС; ∠OMD - искомый.
№ 175 (устно).
V. Подведение итогов
Домашнее задание П. 22 № 167, 170.
2. Решение задач
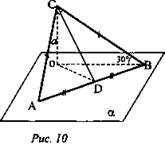
№ 171. Дано: ΔAВС, ∠C = 90°, АС = ВС, АВ лежит в плоскости α, угол между СВ и α 30° (рис. 10).
Найти: угол между плоскостью α и плоскостью треугольника ABC.
Решение:
1) Проведем СО ⊥ α. Тогда ∠CBO = 30°. Пусть в ΔCОВ СО = а, тогда СВ = 2а.
2) Проведем CD ⊥ АВ, тогда АВ ⊥ DO по теореме, обратной теореме о трех перпендикулярах. ∠CDO - искомый угол.
3) Из ACDB, ∠CBD = 45°, CD = CB · sin 45°, CD = a√2. 4) Из ΔCDO: ![]()
![]() (Ответ: 45°.)
(Ответ: 45°.)
№ 175 (устно).
V. Подведение итогов
Домашнее задани.
П. 22 № 167, 170.
№ 167. Дано: DABC - тетраэдр; ![]()
![]() (рис. 11).
(рис. 11).
Доказать: ∠DMB - линейный угол двугранного угла ВACD.
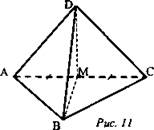
Решение: Так как ΔАВС и ΔADC - равнобедренные, то медианы ВМ и DM являются высотами. Значит, ВМ ⊥ AC, DM ⊥ AC. ∠DMB - линейный угол двугранного угла ВАCD.
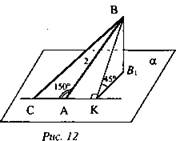
№ 170. Дано: ΔАВС, АС лежит в плоскости α, ![]() двугранный угол ВАСВ1 равен 45° (рис. 12).
двугранный угол ВАСВ1 равен 45° (рис. 12).
Найти: расстояние от точки В до прямой АС и до а.
Решение:
1) ΔABC - тупоугольный (ΔВАС > 150°), поэтому К ∉ АС. Проведем ВК ⊥ СК.
2) Так как AC ⊥ ВК, то AC ⊥ В1К по теореме, обратной теореме о трех перпендикулярах. Значит, ∠BKB1 - линейный угол двугранного угла ВАСВ, ∠BKB1 = 45°.
3) Из ΔВАК: ![]() Из ΔBKB1:
Из ΔBKB1: ![]() (Ответ:
(Ответ: ![]() )
)
Дополнительные задачи
I уровень
Треугольник AВС - прямоугольный ![]()
![]() Чему равен угол между плоскостями ADC и АСВ?
Чему равен угол между плоскостями ADC и АСВ?
Дано: ![]()
Найти: угол между плоскостями ADB и АСВ.
Решение:
1) DK ⊥ АВ, CD ⊥ АВ, значит, СК ⊥ АВ; ∠DKC - искомый.
2) Из ΔАКС: ![]() (катет противолежащей 30°).
(катет противолежащей 30°).
3) Рассмотрим ΔDCK: ![]()
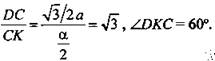 (Ответ: 60°.)
(Ответ: 60°.)
II уровень
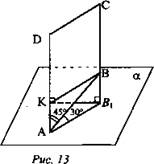
Через сторону ромба ABCD проведена плоскость α.
Сторона АВ составляет с этой плоскостью угол 30°. Найдите угол между плоскостью ромба и плоскостью α, если острый угол ромба равен 45°.
Дано: ABCD - ромб, α, AD лежит в плоскости α, ∠DAB = 45°, угол между плоскостью α и стороной АВ составляет 30° (рис. 13).
Найти: угол между плоскостью ромба и плоскостью α.
Решение:
1. Проведем ВВ1 ⊥ α. Тогда углом между стороной АВ и плоскостью α будет угол BAB1; BK ⊥ AD, ВВ1 ⊥ AD, значит, КВ1 ⊥ AD, ∠BKB1 — угол между плоскостью ромба и плоскостью α.
2. Обозначим АВ = а, тогда ВВ1 = a/2 (противолежащий 30°).
3. Из ΔАКB: ∠A = 45°; ∠K = 90° ⇒ ∠B = 45°. По теореме Пифагора: АВ2 = АК2 + ВК2, а АК = ВК, следовательно, 2ВК2 = АВ2, 2ВК2 = а2, ![]()
4. Из ΔKB1B: ![]() (Ответ: 45°.)
(Ответ: 45°.)