Пирамида - ПИРАМИДА - МНОГОГРАННИКИ

Цели урока:

1) ввести понятие пирамиды;

2) рассмотреть задачи, связанные с пирамидой.

Ход урока

I. Проверка домашнего задания

II. Объяснение нового материала

Одним из важнейших видов многогранников являются пирамиды, с которыми вы уже неоднократно встречались. Еще в младенчестве вы играли игрушкой пирамидой. По истории знакомились с пирамидами Египта (пирамида фараона Хеопса XXVII в. до н. э.). Пирамиды используются в архитектуре (церковь преображения в Кижах, церковь в Каменском).

Дадим определение пирамиды.

Рассмотрим многоугольник А1А2 ... Аn и точку Р, не лежащую в плоскости этого многоугольника, получим и треугольников PA1A2, РА2A3, ..., PAnA1 (1). Многогранник, составленный из n-угольника A1A2 ... Аn и n треугольников (1), называется пирамидой. Многоугольник A1A2 ... Аn называется основанием, треугольники (1) - боковыми гранями пирамиды. Точка Р называется вершиной пирамиды, а отрезки РА1, РА2, ... РАn - ее боковыми ребрами.

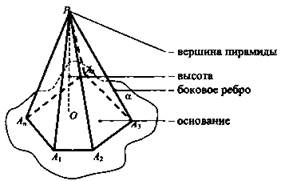
Пирамиду с основанием А1А2 ... Аn и вершиной Р обозначают так: РА1А2 ... Аn, и называют n-угольной пирамидой. Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды PH.

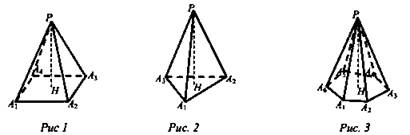
PA1A2A3A4 - четырехугольная пирамида (рис. 1); PA1A2A3 - треугольная пирамида, тетраэдр (рис. 2); PA1A2A3A4A5A6 - шестиугольная пирамида (рис. 3). Перпендикуляр PH - высота (рис. 1, рис. 2, рис. 3).

Площадью полной поверхности пирамиды называется сумма площадей всех ее граней. Площадью боковой поверхности пирамиды - сумма площадей ее боковых граней.

(При объяснении темы использовать модели пирамид.)

III. Закрепление нового материала

1) Устная работа.

а) Что называется пирамидой, основанием пирамиды, боковыми гранями, боковыми ребрами, вершиной?

б) Что называется площадью боковой поверхности пирамиды, площадью полной поверхности пирамиды?

2) Решение задач. № 239 решают ученики у доски, № 247 (a) по готовому чертежу, № 242 (в слабом классе показывает учитель; в сильном классе составить план решения, учащиеся записывают подробное решение в тетрадь самостоятельно).

№ 239

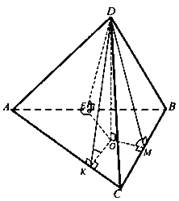
Основанием пирамиды является ромб, сторона которого равна 5 см, а одна из его диагоналей равна 8 см. Найдите боковые ребра пирамиды, если высота ее проходит через точку пересечения диагоналей основания и равна 7 см.

Дано: PABCD - пирамида; ABCD - ромб; АВ = 5 см; АС = 8 см; РН ⊥ АВС, Н - середина диагоналей ромба; PH = 7 см.

Найти: РА; РВ; PC; PD.

Решение:

1. РА из ΔРНА (прямоугольного), (по свойству диагоналей ромба); АН = 4 (см); РА2 = 72 + 42; РА2 = 65 (см);

2. ΔРHA = ΔРHС (АН = НС, PH - общая сторона) , PC = РА.

3. РВ из ΔРНВ (прямоугольного); РВ2 = НВ2 + PH2; НВ из ΔАНВ (прямоугольный, по свойству диагоналей ромба) НВ2 = АВ2 - АН2;

4. РВ = РВ, так как ΔPHD = ΔРНВ (HD = НВ, PH - общая сторона) (Ответ: )

№ 247 а

Двугранные углы при основании пирамиды равны. Докажите, что высота пирамиды проходит через центр окружности, вписанной в основание.

Дано: DABC - пирамида, ∠DMO = ∠DKO = ∠DFO. Доказать О - центр вписанной окружности.

Решение:

1. Двугранные углы DBCA, DACB, DABC при основании пирамиды измеряются линейными углами.

2. ОМ ⊥ ВС; DM ⊥ BC; ∠DMO - линейный угол двугранного угла DBCA; KO ⊥ AC; DK ⊥ AC; ∠DKO - линейный угол двугранного угла DACB.

3. ΔDMO = ΔDKO = ΔDFO (прямоугольные, так как DO - общий катет и по условию ∠DMO = ∠DKO = ∠DFO).

4. Из равенства треугольников следует ОМ = OK = OF. Точка О равноудалена от сторон ΔАВС. Вывод О - центр окружности, вписанной в основание.

№ 242

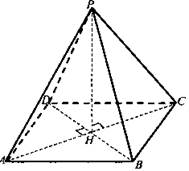
Основанием пирамиды является квадрат, одно из боковых ребер перпендикулярно к плоскости основания. Плоскость боковой грани, не проходящей через высоту пирамиды, наклонена к плоскости основания под углом 45°. Набольшее боковое ребро равно 12 см. Найдите: а) высоту пирамиды; б) площадь боковой поверхности пирамиды.

Дано: PABCD - пирамида (квадрат в основании); PD ⊥ ABC; ΔPCD = 45°; РВ = 12 см.

Найти: a) PD; Sбок..

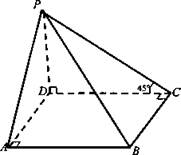
Решение:

1. Боковая грань РСВ образует с плоскостью ABCD двугранный угол с общим ребром ВС. BC ⊥ DC (ABCD - квадрат). ВС ⊥ РС (теорема о трех перпендикулярах). Следовательно, ∠PCD - линейный, ΔРСВ - прямоугольный.

2. ΔPDC - прямоугольный PD ⊥ ABCD; DC = PD, так как ∠PCD = 45°; Обозначим DC = а, получим PD2 + DC2 = PC2; а2 + а2 = РC2; РС = а√2.

3. ΔРСВ - прямоугольный; Значит,

4. ΔADP = ΔCDP (AD = DC, DP — общая сторона);

5. ΔВАР = ΔВСР (АВ = ВС, РВ - общая);

6. (Ответ: )

IV. Подведение итогов

Домашнее задание

I уровень - п. 28, № 243, 240.

II уровень - п. 28, № 240, задача 1.

№ 243

Основанием пирамиды DABC является треугольник ABC, у которого АВ = АС = 13 см, ВС = 10 см, ребро AD перпендикулярно к плоскости основания и равно 9 см. Найдите площадь боковой поверхности.

Дано: DABC - пирамида; ΔАВС - равнобедренный, АВ = АС = 13 см; ВС = 9 см; AD ⊥ ADC, AD = 9 см.

Найти: S6ок..

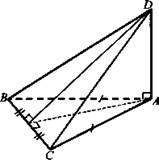
Решение:

1. ΔDAB = ΔDAС (прямоугольные по условию); АС = АВ, DA - общий катет.

2. DK найдем из ΔDAК; DK2 = АК2 + DA2; АК найдем из ΔСКА;

3. (Ответ: 192 см2.)

№ 240

Основанием пирамиды является параллелограмм, стороны которого равны 20 см и 36 см, а площадь равна 360 см2. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 12 см. Найдите площадь боковой поверхности пирамиды.

Дано: PABCD - пирамида, ABCD - параллелограмм; АВ = 20 см; AD = 36 см; SABCD = 360 см2; Н - середина диагоналей AС и BD; PH ⊥ ABCD; PH = 12 см.

Найти: S6ок..

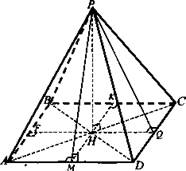
Решение:

1. ΔAPD = ΔВРС; AD = ВС — противоположные стороны параллелограмма, PD = РВ, из равенства ВН и HD наклонные равны, если их проекции, проведенные из одной точки, равны. Треугольники равны по трем сторонам. ΔАРВ = ΔDPC (АВ = DC; АР = PC; PD = CD). Следовательно,

2. S РМ найдем из ΔРНМ; РН = 12 см;

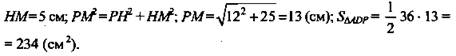
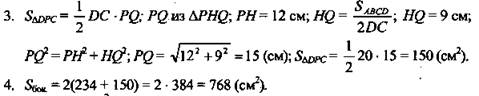
(Ответ: 768 см2.)

Задача 1

В основании пирамиды лежит треугольник со сторонами 10 см, 8 см, 6 см. Боковые ребра наклонены к плоскости основания под углом 45°. Найдите площадь полной поверхности.

Дано: DABC – пирамида, АВ = 10 см, ВС = 6 см, АС = 8 см. ∠DAB = ∠DBA = ∠DCK = 45°.

Найти: Sполн..

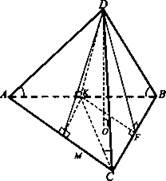
Решение:

1. Так как ребра AD, BD, CD наклонены под одним углом к плоскости основания, то вершина проектируется в центр ΔАВС, ΔАВС - прямоугольный, так как его стороны пропорциональны числам 5, 4, 3. Центр треугольника - точка К делит гипотенузу на два равных отрезка АК = КВ. По условию, ∠DAB = ∠DBA = 45°; ΔHDB - прямоугольный равнобедренный, DK = АК = КВ = 5 см.

3. DF из ΔDKF (прямоугольный); DF2 = DK2 + KF2; KF - средняя линия

4. DM найдем из прямоугольного треугольника DKM; DМ2 = DK2 + MK2; MK - средняя линия;

5. (Ответ: ).