Правильная пирамида - ПИРАМИДА - МНОГОГРАННИКИ

Цели урока:

1) ввести понятие правильной пирамиды;

2) доказать теорему о площади боковой поверхности правильной пирамиды;

3) рассмотреть задачи, связанные с правильной пирамидой.

Ход урока

I. Проверка домашнего задания (собрать тетради)

II. Объяснения нового материала

Пирамида называется правильной, если в основании - правильный многоугольник, а отрезок, соединяющий вершину с центром основания, является ее высотой. Любое боковое ребро представляет собой гипотенузу прямоугольного треугольника, одним катетом которого служит высота пирамиды, а другим - радиус описанной окружности около основания (показать на модели). Следовательно, боковые ребра правильной пирамиды равны друг другу, а боковые грани - равнобедренные треугольники. Основания этих треугольников равны, так как в основании правильный многоугольник. Следовательно, боковые грани равны по третьему признаку равенства треугольников. Высота боковой грани правильной пирамиды, проведенная из вершины, называется апофемой. Все апофемы правильной пирамиды равны друг другу.

Докажите теорему о площади боковой поверхности правильной пирамиды.

Теорема

Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Дано: РА1А2...Аn - правильная пирамида, PN - апофема.

Доказать:

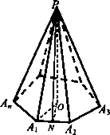
Доказательство: (по определению правильной пирамиды). Что и требовалось доказать.

III. Закрепление нового материала

Устная работа

1. Какая пирамида называется правильной?

2. Докажите, что боковые грани правильной пирамиды равные, боковые ребра равные.

3. Что называется апофемой?

4. Чему равна площадь боковой поверхности?

Решение задач № 254 (а, б), решают ученики у доски. № 264 - в сильном классе комментированием.

№ 254

В правильной треугольной пирамиде сторона основания равна а, высота равна Я. Найдите: а) боковое ребро пирамиды; б) плоский угол при вершине пирамиды.

Дано: DABC - пирамида, ΔАВС - равносторонний, АВ = a, DO = Н.

Найти: a) DA; б) ∠BDC.

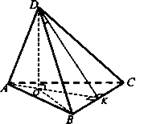
Решение:

1. Так как пирамида правильная, то AD = BD = CD. О - центр треугольника АО = R; ΔAOD - прямоугольный, OD – высота,

2. ΔBDC - равнобедренный, DK - высота, ΔDKB - прямоугольный;

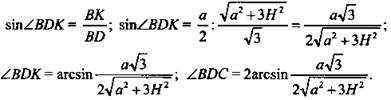
(Ответ: )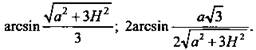

№ 264

Найдите площадь боковой поверхности правильной шестиугольной пирамиды, если сторона основания равна а, а площадь боковой грани равна площади сечения, проведенного через вершину основания.

Дано: MABCDEF - правильная шестиугольная пирамида АВ = a, SΔAMB = SΔAMD.

Найти: S6ок..

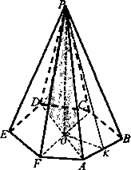
Решение: (так как пирамида правильная), так как получим ΔMОК - прямоугольный, ΔAKO: (Ответ: 3а2.)

IV. Подведение итогов

Домашнее задание

I уровень а: п. 28,29, № 255.

II уровень в: п. 28, 29, № 255, задача 1.

№ 255

В правильной треугольной пирамиде сторона основания равна 8 см, а плоский угол при вершине равен φ. Найдите высоту пирамиды.

Дано: МАВС - правильная пирамида. АВ = 8 см; ∠CMB = φ.

Найти: МО.

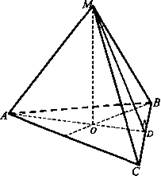
Решение:

1) Так как пирамида правильная, О - центр треугольника АО =R; OD = r, АО = 20D.

2)

3) MD из ΔCDM - прямоугольный,

4) (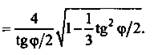Ответ: )

Задача

DABC - правильная треугольная пирамида, сторона основания которой 3√3 см, а боковое ребро - 5 см. МС - медиана ΔАВС.

Найдите площадь ΔMDC.

Дано: DABC - правильная пирамида, АВ = 3√3 , AD = 5 см.

Найти: SΔMDC.

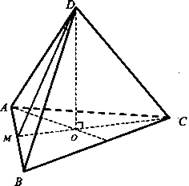
Решение:

1.

2. Так как пирамида правильная, О - центр треугольника,

3. ΔООС - прямоугольный;

4. (Ответ: 9 см2.)

Плакаты № 1, 2, 3, 4, рекомендуемые к урокам № 51, 52, 53 (см. приложение).