Поурочные разработки по геометрии 10 класс
Решение задач по теме «Пирамида» - ПИРАМИДА - МНОГОГРАННИКИ
Цель урока:
- рассмотреть задачи на вычисление площади поверхности произвольной пирамиды.
Ход урока
I. Актуализация знаний
Проверка знаний.
1) Один ученик доказывает теорему.
2) Один ученик у доски решает задачу по планиметрии.
Дано: ΔАВС - правильный, АВ = 3.
Найти: 1) h; 2) r; 3) R; 4) S; 5) х (см. рисунок).
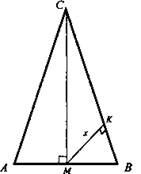
Решение:
1. Пусть ΔАВС данный треугольник; АВ = 3. СМ - высота; ![]()
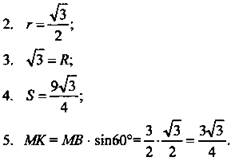
(Ответ: ![]() )
)
Остальные отвечают на вопросы: - Что называется пирамидой? Правильной пирамидой? Что называется площадью боковой поверхности пирамиды? Что называется площадью полной поверхности пирамиды? Чему равна площадь боковой поверхности правильной пирамиды? Как найти радиусы вписанной и описанной окружностей для произвольного треугольника? Формула для площади треугольника?
II. Решение задач
№ 241 (фронтальная работа)
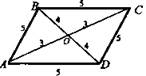
Дано: MADCB - пирамида. АВ = 5 (м), AD = 4 (м), DB = 3 (м), МО = 2 (м).
Найти: Sпир..
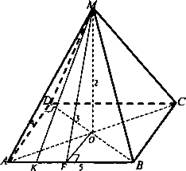
Решение:
1. Пусть АВ = 5 м, AD = 4 м, BD = 3 м. Заметам, что ΔABD - прямоугольный; ∠ADB = 90°; AD ⊥ DO следовательно, по теореме о трех перпендикулярах, AD ⊥ MD, то есть MD является высотой грани MAD.
2. Из ΔMDO получаем: ![]()
3. Из ΔADB имеем DK ⊥ AB, ![]() Из ΔMOF получаем: OF || DK,
Из ΔMOF получаем: OF || DK, ![]()
![]()
4. ![]()
![]() (Ответ:
(Ответ: ![]() )
)
№ 243. Дано: DACB - пирамида; ΔАСВ - треугольник; АВ = АС = 13 см; ВС = 10 см; AD ⊥ ABC; AD = 9 см.
Найти: S6ок..
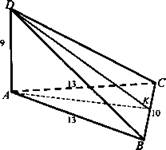
Решение:
1. Проведем AK ⊥ BC, тогда BC ⊥ DK (по теореме о трех перпендикулярах), то есть DK - высота ΔDBC.
2. Из ΔАВК получаем: ![]()
![]()
3. Из ΔDAK имеем: ![]()
4. Из ΔADB = ΔАDC (по двум катетам); ![]()
![]() (Ответ: 192 см2.)
(Ответ: 192 см2.)
IV. Подведение итогов
Домашнее задание
П. 30, п. 29, п. 28.
Задача (1), № 239.
I уровень
Задача (1), № 239
Апофема правильной четырехугольной пирамиды 6 см, высота пирамиды равна 3√2 см. Найдите: а) сторону основания пирамиды; б) угол между боковой гранью и плоскостью основания пирамиды; в) угол, образованный боковым ребром и плоскостью основания пирамиды; г) площадь боковой поверхности пирамиды; д) площадь полной поверхности пирамиды. (Ответы: ![]() )
)
№ 239. Дано: SABCD - пирамида; ABCD - ромб; АВ = CD = ВС = AD = 5 см; BD = 8 см; SO = 7 см.
Найти: AS.
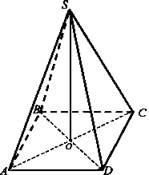
Решение: Пусть SABCD - данная пирамида. ABCD - ромб (по условию задачи). Точка пересечения диагоналей является центром ромба ABCD. О - центр ромба. Следовательно, пирамида является правильной. По свойству диагоналей ромба: DO = ВО = 4 см. ![]() Из ΔASO, по теореме Пифагора, имеем
Из ΔASO, по теореме Пифагора, имеем ![]() SA = SC, как наклонные, имеющие одинаковые проекции. Аналогично из ΔSDO по теореме Пифагора имеем
SA = SC, как наклонные, имеющие одинаковые проекции. Аналогично из ΔSDO по теореме Пифагора имеем ![]() SB = SD - как наклонные, имеющие одинаковые проекции. (Ответ:
SB = SD - как наклонные, имеющие одинаковые проекции. (Ответ: ![]() )
)
II уровен.
№ 250, задача (1)
Дано: ΔАВС; DABC - пирамида; ∠CAB = 120°; DO = 16 см; ∠DAO = 45°.
Найти: SABC.
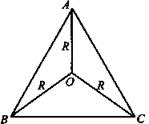
Решение: Основание высоты пирамиды соединяем с вершинами ΔАВС. ΔDOA = ΔDOB = ΔDOC - прямоугольный и равный по катету, DO и углам при вершине D (45°). Тогда AO = OC = OB = OD = 16 (см).
По теореме синусов имеем: ![]()
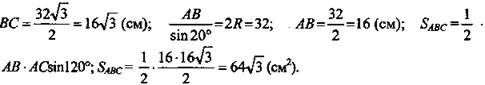
(Ответ: 64√3 см2..
III уровень
№ 245, задача (1)
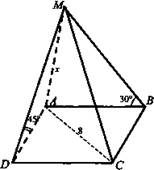
Дано: MABCD - пирамида, ABCD - прямоугольник, АС = 8 см, ∠MDA = 45°, ∠MBA = 30°.
Найти: Sпир..
Решение:
1. Предположим, что плоскости (МАВ) и (MHD) перпендикулярны к плоскости основания, тогда линия их пересечения МА перпендикулярна к плоскости основания, то есть МА - высота пирамиды. Так как СВ ⊥ АВ, то СВ ⊥ MB по теореме о трех перпендикулярах, поэтому ∠MBA - линейный угол двугранного угла при ребре ВС, ∠MBA = 30°.
2. Аналогично AD ⊥ DC, MD ⊥ DC, ∠MDA - линейный угол двугранного угла при ребре DC, ∠MDA = 45°. Треугольники МВС и MDC прямоугольные.
3. Пусть МА = х см, тогда MB = 2х см, АВ = х√3 см. Из ΔMAD имеем: МА = AD = х см, MD = х√2 см. Из ΔАВС получаем: АВ2 + ВС2 = АС2; ![]()

(Ответ: ![]() )
)