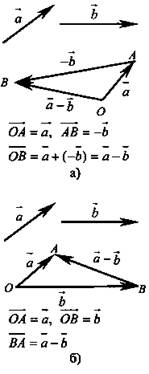Поурочные разработки по геометрии 10 класс
Сложение и вычитание векторов. Сумма нескольких векторов - СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО - ВЕКТОРЫ В ПРОСТРАНСТВЕ
Цели урока:
1) повторить теоретические сведения по теме, изученные в курсе планиметрии;
2) рассмотреть правила треугольника и параллелограмма сложения векторов в пространстве, законы сложения векторов;
3) обратить внимание учащихся на два способа построения разности двух векторов;
4) изучить правило сложения нескольких векторов в пространстве и его применение при нахождении векторных сумм, не прибегая к рисункам.
Ход урока
I. Организационный момент
Постановка целей урока.
II. Повторение с целью подготовки учащихся к восприятию нового материала
Рекомендуется включить в домашнее задание с предыдущего урока повторение п. 80-82 из учебника «Геометрия. 7-9».
К доске вызвать четырёх учащихся для работы по карточкам, составленным таким образом, что задания, входящие в них, охватывают материал по теме «Сложение и вычитание векторов» из планиметрии.
Карточка № 1
1. Даны векторы ![]() Построить вектор
Построить вектор ![]() пользуясь правилом треугольника.
пользуясь правилом треугольника.
2. Рассказать правило треугольника.
3. Упростить выражение ![]()
Карточка № 2
1. Даны векторы ![]() Построить вектор
Построить вектор ![]() пользуясь правилом параллелограмма.
пользуясь правилом параллелограмма.
2. Рассказать правило параллелограмма.
3. Упростить выражение ![]()
Карточка № 3
1. Даны векторы ![]() Построить вектор
Построить вектор ![]()
2. Дать определение разности векторов.
3. Упростить выражение ![]()
Карточка № 4
1. Даны векторы: ![]() Построить вектор
Построить вектор ![]()
2. Рассказать правило сложения нескольких векторов.
3. Упростить выражение ![]()
III. Фронтальная работа с классом / проводится пока учащиеся готовятся у доски
Ученики отвечают на вопросы:
- Что называется вектором в пространстве? Его обозначения.
- Что называется длиной вектора? Ее обозначение.
- Какой вектор называется нулевым?
- Какие векторы называются коллинеарными?
- Какие векторы называются сонаправленными? Обозначение.
- Какие векторы называются противоположно направленными? Обозначение.
- Каким (сонаправленными или противоположно направленным) принять нулевой вектор?
- Какие векторы называются равными?
IV. Изучение нового материала
1. Начнется с прослушивания учащихся, работающих по карточкам.
2. Продолжит учитель, задача которого подчеркнуть, что сложение и вычитание векторов в пространстве вводится так же, как и на плоскости, и подчиняется тем же законам. Затем необходимо выделить из ответов учащихся главное (оставив эти фрагменты на доске), составить опорную схему по теме и дать учащимся время для работы над конспектом в тетради. Примерный вид конспектов:
Сложение и вычитание векторов .
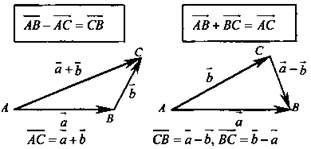
1. Сумма и разность векторов:
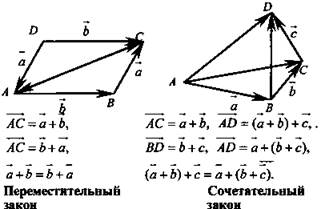
2. Законы сложения векторов:
|
|
|
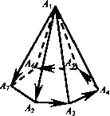
Правило многоугольника можно сформулировать также следующим образом: если Это правило проиллюстрировано на рисунке для т = 7. Отметим, что если точки А1 и Аn, то есть начало первого вектора и конец последнего, совпадают, то сумма векторов равна нулевому вектору.
|
Можно дать творческое задание на дом - объявить конкурс на лучший конспект темы.
V. Закрепление изученного материала
а) Применение знаний в стандартной ситуации.
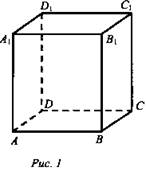
№ 327 (а, б, д) (текст - см. учебник)
(рис. 1). .
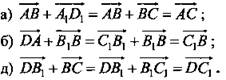
№ 328 а
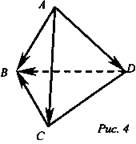
Дан тетраэдр ABCD (рис. 2).
Докажите, что ![]()
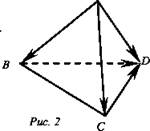
Решение: ![]() следовательно,
следовательно, ![]()
№ 331 а
Пусть ABCD — параллелограмм, а О - произвольная точка пространства.
Докажите, что ![]() (рис. 3).
(рис. 3).
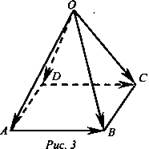
Решение: ![]() Так как ABCD - параллелограмм, то
Так как ABCD - параллелограмм, то ![]() следовательно,
следовательно, ![]() В пространстве даны четыре точки А, В, С и D. Назовите вектор с началом и концом в данных точках, равный сумме векторов
В пространстве даны четыре точки А, В, С и D. Назовите вектор с началом и концом в данных точках, равный сумме векторов ![]()
Решение: ![]()
![]()
![]()
б) Самостоятельная работа обучающего характера с последующей самопроверкой (решение на обратной стороне доски)
№ 379, 380 (Текст - см. учебник)
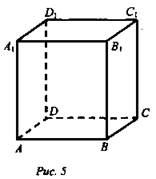
(рис. 4).
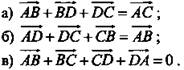
(рис. 5)
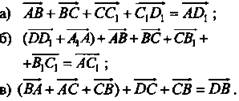
VI. Подведение итогов
В конце урока желательно с помощью ребят перечислить понятия, правила, свойства, которые были рассмотрены на уроке и которые необходимо запомнить.
Домашнее задание
П. 36,37.
I уровень: № 327 (в, г); 330 (а, б); 335 (а, б);
II уровень: № 327 (е); 330 (в, г, д); 335 (в, г); № 340; - конспект темы.