Решение задач на применение аксиом стереометрии и их следствий. Самостоятельная работа - АКСИОМЫ СТЕРЕОМЕТРИИ И ИХ СЛЕДСТВИЯ

Цель урока:

- закрепить усвоение вопросов теории в процессе решения; проверить уровень подготовленности учащихся путем проведения самостоятельной работы контролирующего характера.

Ход урока

I. Организационный момент

II. Проверка домашнего задания

Учитель отвечает на вопросы учащихся. У нескольких учащихся взять на проверку тетради с домашней работой.

III. Решение задач на повторение теории (п. 1-3) на доск.

Задача № 1

Стороны АВ и АС треугольника ABC лежат в плоскости α. Докажите, что и медиана лежит в плоскости α (рис. 1).

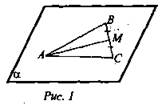
Решение: В ходе решения этой задачи повторяются формулировки аксиом и следствий из них.

1. Так как АВ принадлежит плоскости α, то точка В принадлежит плоскости α. Аналогично точка С принадлежит плоскости α.

2. По аксиоме А2 сторона ВС принадлежит плоскости α. Так как точка М принадлежит стороне ВС, то точка М принадлежит плоскости α.

3. Точка А принадлежит α и точка М принадлежит плоскости α. По аксиоме А2, медиана АМ принадлежит плоскости α.

Задача № 2

В чем ошибка чертежа, где О ∈ EF. Дайте объяснение. Сделайте верный чертеж. (Ответ: )

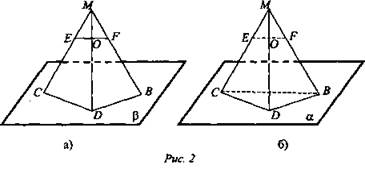
Самостоятельная работа (20 мин) (см. приложение.

Ответы к самостоятельной работе

		1	2	3
		а	б	в
I уровень	I	S, К, М, А	ABC	SC	Да	Точка принадлежит прямой
	II	А, С, М, N	ASB	AC	Да	Лежат на одной прямой
II уровень	I	ABC и DEF	EF	ABC	Нет	Пересекаются
	II	SBC и DEF	DE	ABS	Да	Пересекаются
III уровень	I	ВС1С и В1А1С	A1D	AA1B	Да	Лежат на одной прямой
	II	А1В1А и A1B1D	АВ1	AA1D	Нет	Лежат на одной прямой

IV. Подведение итогов

1. Собрать тетради с самостоятельной работой.

2. Оценки за урок.

Домашнее задание

П. 1-3. В каждом из уровней решить противоположный вариант.

I уровень

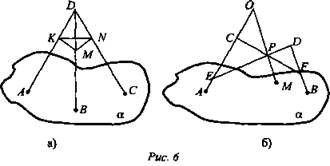
II уровень

Вариант I

№ 2. Дано: a ∩ b = 0, b ∩ c = 0, c ∩ a = 0 (рис. 7).

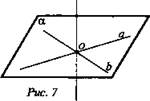
Решение: Две прямые обязательно лежат в одной плоскости (следствие из аксиом), а третья прямая может как лежать, так и не лежать в плоскости а. а ⊂ α, b ⊂ α, с ⊂ α - ? (Ответ: Нет.)

№ 3. Дано: α ∩ β = с, а ⊂ α, а ∩ β = А (рис. 8). Каково взаимное расположение а и с - .

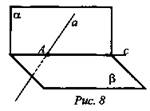
Решение:

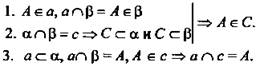
(Ответ: а пересекается с прямой с в точке А.)

Вариант II

№ 2. Дано: а ∩ b, b ∩ с, с ∩ а (рис. 9). а ⊂ α, b ⊂ α, с ⊂ α - ?

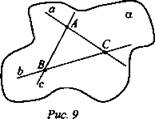
Решение:

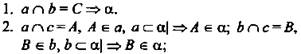
№ 3. Дано: А ∩ α, В ∈ а, А ∈ с, В ∈ с | ⇒ (аксиома А2) С ⊂ α А ∈ α; А ∈ α, В ∈ α, А ∈ с, В ∈ с ⇒ с ⊂ α. (Ответ: Да.)

№ 3. Дано: α ∩ β = с, А ⊂ α, а ∩ с = А, а ∩ С = А, А ∈ а, а ⊂ α | А ∈ α (рис. 10).

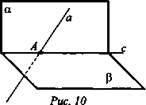
Каково взаимное расположение прямой а и плоскости β - ?

Решение:

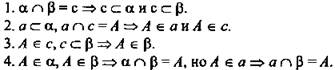
(Ответ: прямая а пересекает плоскость β.)

III уровень

Вариант I

№ 2. Дано: a ∩ β, b ∩ с, а ⊂ α, с ∩ d, а ∩ с, b ⊂ α, а ∩ d, b ∩ d, с ⊂ α, d ⊂ α (рис. 11).

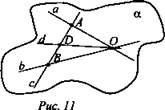
Решение:

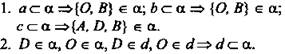
(Ответ: Да.)

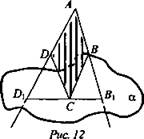
№ 3. Дано: ABCD — четырехугольник (рис. 12),

Каково взаимное расположение точек С, В1, D1 - ?

Решение:

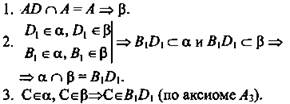
(Ответ: точки В1Д1 и С лежат на одной прямой.)

Вариант II

№ 2. Дано: (рис. 13).

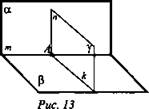
Верно ли, что данные плоскости имеют общую прямую?

Решение:

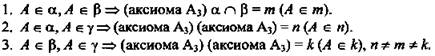
(Ответ: Нет.)

№ 3. Дано: (рис. 14).

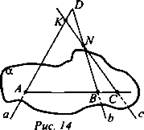
Каково взаимное расположение точек А, В, С - ?

Решение:

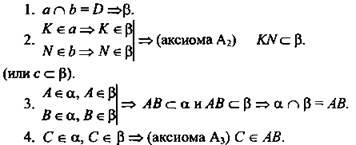
(Ответ: точки А, В и С лежат на одной прямой.)