Поурочные разработки по геометрии 10 класс
Компланарные векторы. Правило параллелепипеда - КОМПЛАНАРНЫЕ ВЕКТОРЫ - ВЕКТОРЫ В ПРОСТРАНСТВЕ
Цели урока:
1) ввести определение компланарных векторов;
2) рассмотреть признак компланарности трех векторов и правило параллелепипеда, сложение трех некомпланарных векторов.
Ход урока
I. Организационный момент
II. Постановка целей и мотивация урока
III. Объяснение нового материала
Определение
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. Любые два вектора компланарны; три вектора, среди которых два коллинеарные, также компланарны (объясните почему).
Пример: рис. 1.
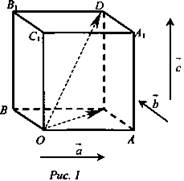
На рис. 1 изображен параллелепипед.
Векторы ![]() - компланарны, так как, если отложить от точки О вектор, равный
- компланарны, так как, если отложить от точки О вектор, равный ![]() то получится вектор
то получится вектор ![]() а векторы
а векторы ![]() лежат в плоскости ОСЕ.
лежат в плоскости ОСЕ. ![]() - некомпланарны, так как вектор
- некомпланарны, так как вектор ![]() не лежит в плоскости ОАВ. Признак компланарности 3-х векторов: если вектор
не лежит в плоскости ОАВ. Признак компланарности 3-х векторов: если вектор ![]() можно разложить по векторам
можно разложить по векторам ![]() то есть представить в виде:
то есть представить в виде: ![]() (х, у - некоторые числа), то векторы
(х, у - некоторые числа), то векторы ![]() - компланарны.
- компланарны.
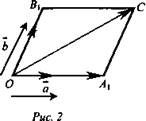
Доказательство: Пусть ![]() не коллинеарные (рис. 2) (если коллинеарные - компланарность очевидна). Отложим отточки О векторы:
не коллинеарные (рис. 2) (если коллинеарные - компланарность очевидна). Отложим отточки О векторы: ![]() и
и ![]() лежат в плоскости ОАВ. В плоскости ОАВ лежат и векторы
лежат в плоскости ОАВ. В плоскости ОАВ лежат и векторы ![]() и
и ![]() лежит в той же плоскости.
лежит в той же плоскости. ![]() Что и требовалось доказать. Обратное утверждение: если векторы
Что и требовалось доказать. Обратное утверждение: если векторы ![]() компланарны, а векторы
компланарны, а векторы ![]() некомпланарны, то вектор
некомпланарны, то вектор ![]() можно разложить по векторам
можно разложить по векторам ![]() то есть
то есть ![]() причем коэффициенты х и у определяются единственным образом.
причем коэффициенты х и у определяются единственным образом.
Доказательство: (самостоятельно) на основании теоремы о разложении вектора по двум неколлинеарным векторам.
1) ![]() - компланарны (по условию).
- компланарны (по условию).
Если их отложить от точки А, то они будут лежать в одной плоскости.
2) Построим параллелограмм ABCD: ![]()
3) ![]() коллинеарные
коллинеарные ![]() аналогично
аналогично ![]()
4) ![]() что и требовалось доказать (единственность коэффициентов х, у доказать самостоятельно дома).
что и требовалось доказать (единственность коэффициентов х, у доказать самостоятельно дома).
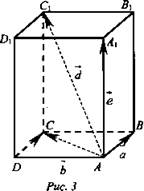
Правило параллелепипеда (для сложения трех некомпланарных векторов).
Дано: ![]() (рис. 3).
(рис. 3).
![]()
IV. Формирование знаний и умений
Устно - № 355 а) да; б) нет; в) да; г) нет.
У доски - № 356.
Дано: ![]() (рис. 4).
(рис. 4).
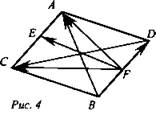
1) Доказательство: ![]()
2) ![]() - компланарны - ?
- компланарны - ?
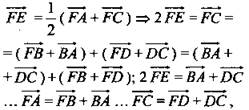
согласно признаку компланарности, векторы ![]() компланарны.
компланарны.
Решение упражнений № 359 a) ![]()
![]()
V. Подведение итогов
(по вопросам 13, 14, 15, стр. 92)
Домашнее задание
№ 358, 359 (б); доп. 368, (а, б)
Ответ к д/з № 358 ![]()
№ 359 б) ![]()
№ 368 а) ![]() б)
б) ![]()