Зачет по теме «Векторы в пространстве» - КОМПЛАНАРНЫЕ ВЕКТОРЫ - ВЕКТОРЫ В ПРОСТРАНСТВЕ

Цель урока:

- выявить уровень знаний учащихся по теме «Векторы в пространстве». Ход урока

I. Организационный момент

II. Проведение зачета

Карточки с заданиям.

I уровень

Вариант I

№ 1. Вопрос. Сформулируйте определения вектора, его длины, коллинеарности двух ненулевых векторов, равенства векторов. Проиллюстрируйте их, используя изображения параллелепипеда.

№ 2. Задача. На рисунке изображен тетраэдр ABC, ребра которого равны. Точки М, N, P и Q- середины сторон АВ, AD, DC, ВС; а) выпишите все пары равных векторов, изображенных на этом рисунке; б) определите вид четырехугольника MNPQ.

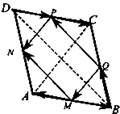
Решение:

а)

б) Так как NP и MQ - средние линии в ΔADC и ΔАВС, то NP = MQ, следовательно, MN - средняя линия ΔADB; a PQ - средняя линия ΔCBD; MN = PQ = 1/2BD. Так как все ребра тетраэдра равны, то тетраэдр - правильный, а в правильном тетраэдре скрещивающиеся ребра взаимно перпендикулярны. Тогда, BD ⊥ AC; 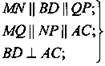четырехугольник MNPQ - квадрат.

(Ответ: a) б) квадрат.)

№ 3. Задача. Дан параллелепипед MNPQM1N1P1Q1. Докажите, что

Дано: MNPQM1N1P1Q1 - параллелепипед.

Доказать:

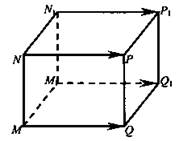
Решение: так как MNPQM1N1P1Q1 - параллелепипед, а ребра MQ и M1N1 параллельны и равны. Аналогично доказывается и так как противоположные стороны параллелограммов MNPQ и M1N1P1Q1 соответственно. Складывая левые и правые части равенств, получим что и требовалось доказать.

Вариант II

№ 1. Вопрос. Расскажите о правиле треугольника сложения двух векторов. Проиллюстрируйте эти правила на рисунке.

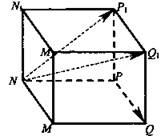
№ 2. Задача. Упростите выражение:

Решение:

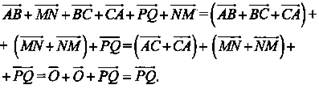
№ 3. Задача. Дан параллелепипед MNPQM1N1P1Q1. Докажите, что

Дано: MNPQM1N1P1Q1 - параллелепипед.

Доказать:

Решение: Таким образом,

II уровень

Вариант I

№ 1. Вопрос. Расскажите о правиле параллелограмма сложения двух векторов. Проиллюстрируйте это правило на рисунке.

№ 2. Задача. Дана треугольная призма ABCA1B1С1. Укажите вектор начало и конец которого являются вершинами призмы, такой, что

Дано: ABCA1B1С1 - треугольная призма.

Найти:

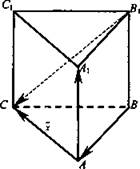
Решение: поэтому

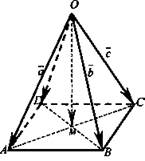
№ 3. Задача. Основанием пирамиды с вершиной О является параллелограмм ABCD, диагонали которого пересекаются в точке М. Разложите векторы по векторам

Решение: тогда Значит.

(Ответ: )

Вариант II

№ 1. Вопрос. Расскажите о правиле многоугольника сложения нескольких векторов. Проиллюстрируйте его на рисунке.

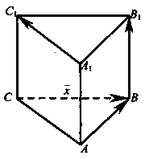
№ 2. Задача. Дана треугольная призма ABCA1B1С1. Укажите вектор начало и конец которого являются вершинами призмы, такой, что

Решение: а так как (Ответ: )

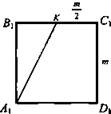
№ 3. Задача. Точка К - середина ребра В1С1 куба ABCDA1B1C1D. Разложите вектор по векторам и найдите длину этого вектора, если ребро куба равно m.

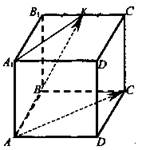
Решение: Имеем: то есть так как Построим отрезок А1К. Для ΔАА1К по теореме Пифагора:

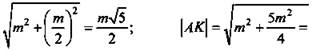
(Ответ: )

III уровень

Вариант I

№ 1. Вопрос. Сформулируйте определение произведения вектора на число к, сочетательный, первый и второй распределительные законы умножения вектора на число. Проиллюстрируйте их на примерах.

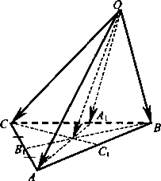
№ 2. Задача. На рисунке изображен правильный октаэдр. Докажите, что

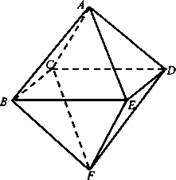
Решение: так как векторы принадлежат одной плоскости, их длины равны, a ABFD - параллелограмм или

№ 3. Задача. Точки А1, В1, С1 - середины сторон ВС, АС, АВ треугольника ABC, точка О - произвольная точка пространства. Докажите, что

Решение: значит, Запишем аналогичные равенства для других граней. и Складывая эти три равенства, получим: что и требовалось доказать.

Вариант II

№ 1. Вопрос. Сформулируйте определение компланарных векторов. Приведите примеры компланарных и некомпланарных векторов, используя изображение параллелепипеда.

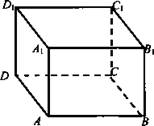
№ 2. Задача. Дан параллелепипед AABCDA1B1C1D1. Найдите сумму векторов

Решение:

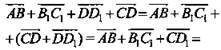
(Ответ: )

№ 3. Задача. В тетраэдре ABCD точка К - середина медианы ВВ1 грани BCD. Разложите вектор по векторам

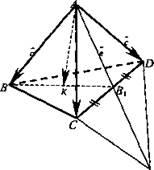
Решение. Проведем следовательно, имеем равенство: Достроим ΔACD до параллелограмма; сложив и по правилу параллелограмма, получим, что их сумма равна диагонали параллелограмма, выходящей из вершины А. Но эта диагональ равна Значит, Таким образом, (Ответ: )

Дополнительные вопросы:

1. Сформулируйте и докажите утверждение, выражающее признак компланарности трех векторов.

2. Расскажите о правиле параллелепипеда сложения трех некомпланарных векторов. Проиллюстрируйте его на рисунке.

3. Сформулируйте теорему о разложении вектора по трем некомпланарным векторам.

III. Подведение итогов