Итоговое повторение. Аксиомы стереометрии и их следствия - ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ

Цель урока:

1) провести диагностику знаний учащихся;

2) повторить, систематизировать и обобщить знания по теме урока.

Ход урока

I. Организационный момент

II. Актуализация знаний учащихся

Учащиеся самостоятельно работают с таблицей 1 и с учебником (стр. 4-7) в течение 3-х минут.

III. Теоретический тест с последующей самопроверкой (см. приложение)

Вариант	1	2	3	4	5	6	7	8	9	10
I	д	д	в	в	б	г	а	б	д	в
II	г	д	а	а	б	г	а	г	б	в

Обсуждаются ответы, которые вызывают вопрос у учащихся. При необходимости проводятся индивидуальные консультации.

IV. Решение задач

Сильные учащиеся работают самостоятельно. Учитель контролирует работу слабых учащихся, оказывая необходимую помощь, либо задачи решаются у доски по готовым чертежам, то есть ведется фронтальная работа с учащимися.

Задачи на готовые чертежах: 1, 3, 4 или 5, 6, 7.

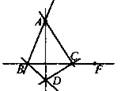
1. Дано: точки А, В, С не лежат в одной плоскости.

Указать.

1) плоскости, которым принадлежат: а) прямая АВ; б) точка F; в) точка С.

2) прямую пересечения плоскостей: a) ABC и ACD; б) ABD и DCF.

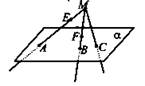
2. Дано:

1)

2) Может ли

3) Указать прямую пересечения плоскостей: а) α и MBA; б) АВМ и ВМС.

4) принадлежит ли А С плоскости МВС?

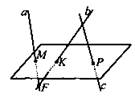
3. Дано: прямые а, b и с пересекают α в точках М, К и Р.

Лежат ли прямые а, b и с в одной плоскости?

4. Дано: прямая с - линия пересечения плоскостей α и β,

Доказать: а и b не лежат в одной плоскости.

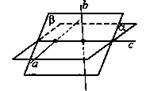
Доказательство: Предположим противное: пусть а и b лежат в одной плоскости. Тогда с принадлежит этой плоскости. Через а и с проведем единственную плоскость α, которая ∈ b - противоречие.

5. Дано:

Построить прямые пересечения плоскости ABC с плоскостями α и β.

6. Дано: Куб ABCDA1B1C1D1; К ∈ DD1. Постройте: а) точку пересечения АК1 с плоскостью α; б) С1 ∩ α в точке - ? в) прямую пересечения A1C1 и плоскости α.

Решение: а) А1К и АВ лежат в одной плоскости и не параллельны. Значит, б) С1К ∩ α в точке, расположенной на продолжении СВ.

7. Дано: МАВС - тетраэдр,

1) Назовите прямую, по которой пересекаются плоскости: а) МАВ и MFC; б) MCF и ABC.

2) Найти длину CF и SΔABC.

3) Как построить точку пересечения DE с плоскостью ΔАВС?

8. Дано: ABCDA1B1C1D1 - куб; Р ∈ ВВ1, В1Р = РВ.

1) Построить точку пересечения D1P и плоскости ABC.

2) Как построить линию пересечения AD1P и АВВ1.

3) Вычислить длину отрезков АР и A1D1, если АВ = а.

Ответы и указания:

3. Нет. Если бы а, b, и с лежали бы на одной прямой.

5. Прямая пересечения плоскостей ABC и β проходит через точку С и точку пересечения прямых АВ и а, если АВ ∩ а = F, то (ABC) ∩ β = CF.

6. (в) С1К продолжить до пересечения с СВ, пусть С1К ∩ СВ = М, М ∈ а, пусть

7. 1. а) (МАВ) ∩ (MFC) = MF, так как М ∈ МАВ, М ∈ MFC, F ∈ МАВ; б) (MCF) ∩ (ABC) = FC, аналогично. 2. в) так как ΔFBC - прямоугольный, ∠F = 90°; CF - медиана и высота ΔАВС. 3. DE и ВС лежат в одной плоскости. Пусть они пресекаются в точке К, так как К ∈ ВС, значит, К ∈ ABC.

8. Решение:

Количество задач достаточно для работы в классе и дома. Поэтому отставшие от классной работы ученики, задачи решают дома.

IV. Подведение итогов

Домашнее задание

2; 4; 8; повторить п. 1 (4-11).