Поурочные разработки по геометрии 10 класс
Контрольная работа № 5 - ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ
Цель урока:
- проверка знаний и умений учащихся.
Ход урока
I. Организационный момент
II. Решение контрольной работы (см. приложение)
III. Подведение итого.
Краткое решение
I уровень
Вариант I
1. а) ![]() (правило многоугольника),
(правило многоугольника), ![]() - это длина отрезка АВ. Рассмотрим треугольник ABC: угол В равен 90°, используя теорему Пифагора, получим
- это длина отрезка АВ. Рассмотрим треугольник ABC: угол В равен 90°, используя теорему Пифагора, получим ![]()
б) Угол между прямой и плоскостью - это угол между прямой и проекцией прямой на эту плоскость. Искомый угол ∠SBA = 45° из треугольника SAB ∠A = 90°, SA = АВ = 12 см, тогда треугольник равнобедренный и углы при основании 45°.
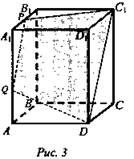
2. а) В основании пирамиды ABCD квадрат ![]()
б) ОМ - радиус вписанной окружности, ![]()
в) Треугольник SOM: ![]()
г) ![]()
3. а) Плоскость сечения пересекает грань AA1D1D по прямой DQ, а плоскость AA1B1B по прямой QP.
б) QP принадлежит плоскости АА1В1В, но эта плоскость параллельна плоскости DD1C1C. Параллельные плоскости пересекаются третьей по параллельным прямым. Поэтому плоскость сечения пересечет плоскость DD1C1C по прямой, параллельной QP и проходящей через точку D, через DC1.
Вариант II
1. a) ![]() длину отрезка найдем по теореме Пифагора
длину отрезка найдем по теореме Пифагора ![]()
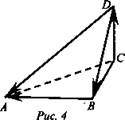
б) Треугольник ACS равнобедренный прямоугольный, ∠A = 45°.
2. Треугольник SOP: ![]()
![]()
![]()
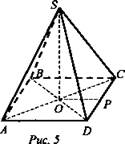
3. AB принадлежит сечению, тогда ABCD пересекается по АВ1 и АА1В1В пересекается по АВ. ВВ1С1С пересекает по BQ. Плоскости ABCD и A1B1C1D1 параллельны, тогда сечение пересекает верхнюю грань по прямой, параллельной АВ, QE параллельно АВ, Е - середина A1D1. EQBA - искомое сечение, параллелограмм.
II уровень
Вариант I
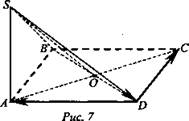
1. BD ⊥ AO (диагонали ромба пересекаются под прямым углом) и SO ⊥ BD по теореме о трех перпендикулярах. Тогда BD ⊥ SAO, так как перпендикулярна двум пересекающимся прямым из этой плоскости (рис. 7). ![]()
![]() Найдем длину отрезка SO по теореме Пифагора:
Найдем длину отрезка SO по теореме Пифагора: ![]() Плоский угол двугранного угла SDBA: ∠SOA = 60°, из треугольника SOA sin-
Плоский угол двугранного угла SDBA: ∠SOA = 60°, из треугольника SOA sin-![]()
2. Рассмотрим треугольник SAB, равнобедренный, углы при основании равны, ∠S = 120°, ∠A = ∠B = 30° (рис. 8).
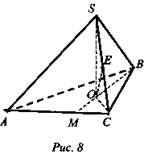
Рассмотрим треугольник SOC: ОМ = SM = ME = 3 см, как радиусы описанной окружности. SC= 6 см.
Рассмотрим треугольник SCM, ∠M = 90°, ∠C = 30°, SM = 3 см и МС = 3√3, в треугольнике SAC: ![]()
![]()
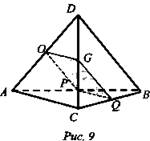
3. О - середина AD и Q - середина ВС (рис. 9). Провели РО, GO параллельно BD. POGQ - искомое сечение, параллелограмм. По теореме о средней линии имеем ![]()
![]() - противолежащие стороны равны из равенства ребер тетраэдра, сечение параллелограмма.
- противолежащие стороны равны из равенства ребер тетраэдра, сечение параллелограмма.
Вариант II
1. (рис. 10) AO ⊥ BD; BD ⊥ SO, плоскости SBD и SAO перпендикулярны по признаку.
![]()
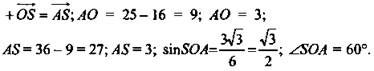
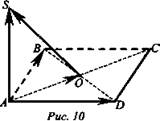
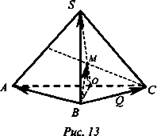
2. Рассмотрим треугольник SOC: OP = SP = СР = 3 см, как радиусы описанной окружности, SC = 6 см и ∠C = 60°, тогда ОС = SC cos60° = 3. Вычислим АВ, зная что ОС - радиус вписанной окружности, ![]()
![]()
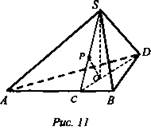
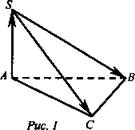
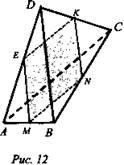
В плоскости АВС провели через точку М прямую параллельную АС, она пересекла ВС в точке N. По теореме Фалеса, N - середина ВС, MN - средняя линия в треугольнике ABC, тогда MN параллельно АС.
1) В плоскости ADC провели через точку Е прямую, параллельную АС, она пересекла DC в точке К. По теореме Фалеса, К - середина DC; ЕК - средняя линия в треугольнике ADC, тогда ЕК параллельно А С.
2) MN параллельно АС и ЕК параллельна АС по теореме о двух параллельных прямых третьей, тогда MN параллельно АК. Провели через параллельные прямые MN и АК плоскость, она существует и единственна. MN и КЕ - искомое сечения. Сечение параллельно АС по признаку параллельности прямой и плоскости.
III уровень
Вариант I
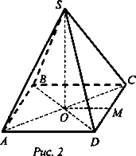
1. a) SB ⊥ АВ и АВ ⊥ ВС, тогда по признаку перпендикулярности прямой и плоскости AB ∈ SBC, AB ∈ SAB, тогда по признаку перпендикулярности плоскостей SAB ⊥ SBC.
б) Пусть ![]() По правилу сложения векторов
По правилу сложения векторов
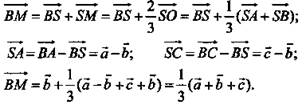
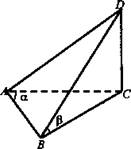
1) Рассмотрим треугольник BDC: ∠B = 90°, ![]()
2) Рассмотрим ![]()
3) Рассмотрим треугольник DBC: ![]()
4) Рассмотрим треугольник DCA: ∠C = 90°, так как DC перпендикулярно по теореме о трех перпендикулярах. ![]()
5) ![]()
2. 1) В грани SCD провели NK параллельно SD. К - середина CS.
2) В грани SAD провели РК параллельно SD. М - середина SA.
3) PNKM - искомое сечение.
Вариант II
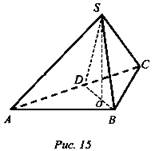
1. 1) AC ⊥ BD, так как медиана в равнобедренном треугольнике ABC и высота. Треугольник ASC равнобедренный, ВА = ВС являются проекциями SA и SC. Тогда АС перпендикулярно плоскости SBD, значит, плоскости SAC и SBD тоже перпендикулярны.
![]()
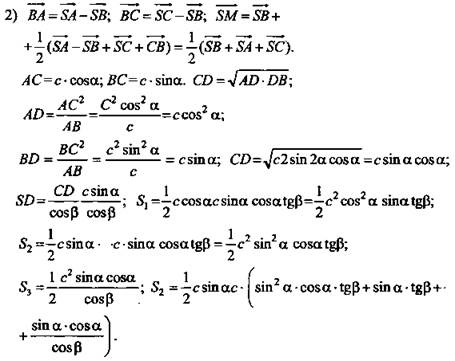
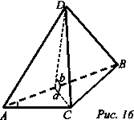
2. 1) провели в плоскости ACD, MN параллельно AС;
2) в треугольнике SAC провели ЕК параллельно АС;
3) EKNM - искомое сечение.