Поурочные разработки по Геометрии 11 класс
Повторение вопросов теории и решение задач - Скалярное произведение векторов - МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
Цель урока:
- повторить формулы скалярного произведения в координатах, косинуса угла между данными векторами через их координаты, косинуса угла между двумя прямыми, между прямой и плоскостью.
Ход урока
I. Актуализация опорных знаний
Консультанты докладывают о результатах проверки домашнего задания и один ученик у доски записывает решение № 467 б).
Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед, АВ = ВС = 1/2AA1 (рис. 1).
Найти: (АС, АС1).
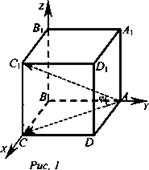
Решение: А(0; 1; 0), C(1; 0; 0), ![]() {1; -1; 0}, С1(1; 0; 2),
{1; -1; 0}, С1(1; 0; 2), ![]() {1; -1; 2}.
{1; -1; 2}. ![]()
![]()
![]() (Ответ: 54,7°.)
(Ответ: 54,7°.)
Второй ученик заполняет на доске пропуски в формулах: ![]() коллинеарные, значит,
коллинеарные, значит, ![]() k - некоторое число, г) если
k - некоторое число, г) если ![]() неколлинеарные, то
неколлинеарные, то ![]()
![]()
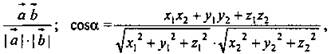 ж) если
ж) если ![]() тo
тo ![]()
Остальные отвечают на вопросы:
- Как находят координаты вектора, если известны координаты его начала и конца?
- Как находят координаты середины отрезка? Длины вектора? Расстояние между точками?
- Как вы понимаете выражение «угол между векторами»?
- Какие векторы называются перпендикулярными?
- Что называется скалярным произведением векторов?
- Чему равно скалярное произведение перпендикулярных векторов?
- Чему равен скалярный квадрат вектора?
- Свойства скалярного произведения?
- Какой вектор называется направляющим вектором прямой а?
После фронтального опроса проверяется работа второго ученика (у доски) и предлагается всем учащимся самостоятельно разобрать решение задачи № 469 (а) (с последующей проверкой).
Задача № 469 а) (по задаче 2 из п. 48).
Дано: ABCDA1B1C1D1 – куб, AC ∩ BD = N, = М ∈ A1D1, А1М: MD1 = 1 : 4 (рис. 2).
Найти: синус угла между MN и плоскостью ABCD.
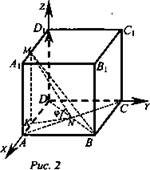
Решение (см. рисунок): Введем систему координат. Найдем координаты направляющего вектора прямой MN и координаты вектора, перпендикулярного плоскости грани ABCD. Пусть А(1; 0; 0), тогда М(4/5; 0; 1), MK ⊥ AD, К(4/5; 0; 0), ![]() {0; 0; 1}; N(1/2; 1/2; 0);
{0; 0; 1}; N(1/2; 1/2; 0);
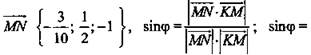
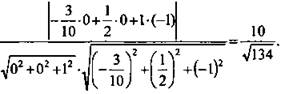 (Ответ:
(Ответ: ![]() )
)
Наиболее подготовленному ученику предлагается выполнить № 469 (а) на переносной доске с последующим разбором этого задания всем классом (при необходимости).
II. Формирование умений и навыков учащихся
Совместное решение № 471, 472 (при наличии времени - чертеж заготовлен заранее; можно предложить проговорить и записать кратко решение на доске).
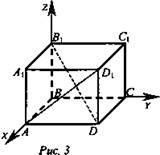
№ 471. Дано: ABCDA1B1C1D1 - куб (рис. 3).
Доказать: ![]()
Доказательство:
1. Введем систему координат.
2. В(0; 0; 0), А(а; 0; 0), D(a; a; 0), D1(а; а; а), В1(0; 0; а).
3. ![]() {0; a; a);
{0; a; a); ![]() {-а; -а; а}.
{-а; -а; а}.
![]()
![]() Значит
Значит ![]() то есть AD1 ⊥ DB1.
то есть AD1 ⊥ DB1.
№ 472. (кратко) - обговорить идею решения, краткая запись решения.
Дано: MNPQM1N1P1Q1 - куб (рис. 4).
Доказать: PM1 ⊥ (MN1Q1); PM1 ⊥ (QNP1).
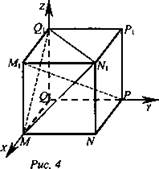
Доказательство: Введем систему координат. Идея решения. Найти координаты векторов ![]() доказать с помощью скалярного произведения, что MN1 ⊥ РМ1 и MQ1 ⊥ РМ; сделать вывод по признаку перпендикулярности прямой и плоскости, что PM1 ⊥ (MN1Q1).
доказать с помощью скалярного произведения, что MN1 ⊥ РМ1 и MQ1 ⊥ РМ; сделать вывод по признаку перпендикулярности прямой и плоскости, что PM1 ⊥ (MN1Q1).
Решение: M(1; 0; 0), N1(1; 1; 1), Q1(0; 0; 1), M1(1; 0; 1), ![]() {0; 1; 1},
{0; 1; 1}, ![]() {-1; 0; 1},
{-1; 0; 1}, ![]() {1; -1; 1},
{1; -1; 1}, ![]() Значит,
Значит, ![]() и MN1 ⊥ PM1.
и MN1 ⊥ PM1. ![]()
![]() Значит,
Значит, ![]() и MQ1 ⊥ PM1. Поэтому PM1 ⊥ (MN1Q1).
и MQ1 ⊥ PM1. Поэтому PM1 ⊥ (MN1Q1).
Аналогично доказывается, что PM1 ⊥ (QNP1).
III. Самостоятельная работа (5-7 мин.)
Уровень А
Вариант I
Даны векторы ![]()
Вычислите ![]() (Ответ: 6).
(Ответ: 6).
Вариант II
Даны векторы ![]()
Вычислите ![]() (Ответ: 2).
(Ответ: 2).
Решение:
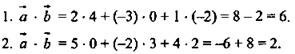
Уровень Б
Вариант I
Вычислить угол между прямыми AB и CD, если А(√3; 1; 0), В(0; 0; 2√2), С(0; 2; 0), D(√3; 1; 2√2). (Ответ: 60°.)
Вариант II
Вычислите угол между прямыми АВ и CD, если А(6; -4; 8), В(8; -2; 4), С(12; -6; 4), D(14; -6; 2). (Ответ: 30°).
Решение:
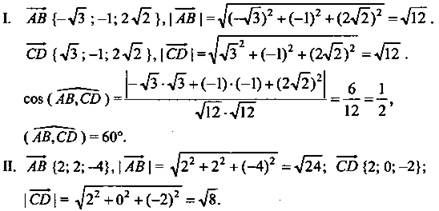
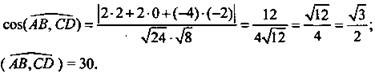
Уровень В
Вариант I
В кубе ABCDA1B1C1D1 диагонали грани ABCD пересекается в точке N, а точка M ежит на ребре A1D1, причем А1М : MD1 = 1 : 4.
Вычислите синус угла между прямой MN и плоскостью грани DD1C1C[AA1D1D].
(Ответы: ![]() .)
.)
Вариант II
№ 469 (б) - I, (в) - II.
Дано: ABCDA1B1C1D1 - куб, AC ∩ BD = N, M ∈ A1D1, А1М : MD1 = 1 : 4 (рис. 5).
Найти: б) sin(MN,(DD1C1C)), в) ![]()
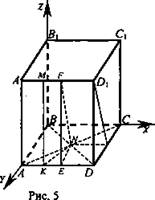
Решение: Введем систему координат так, чтобы В(0; 0; 0), АВ ∈ ох, ВС ∈ оу, ВВ1 ∈ oz, А(а; 0; 0), С(0; а; 0), D(а; а; 0), В1(0; 0; а), А1(а; 0; а), С(0; a; a), A (a; a; a), D1(а; а; а), М(а; a/5; a), N(a/2; a/2; 0).
Угол между прямой и плоскостью.
Угол между прямой и ее проекцией на эту плоскость.
б) ![]() В ΔMFN:
В ΔMFN: ![]() так как
так как ![]()
![]() Значит,
Значит, ![]() (Ответ:
(Ответ: ![]() .)
.)
в) Аналогично, ![]()
![]() (Ответ:
(Ответ: ![]() .)
.)
IV. Подведение итогов
- Мы отработали умение применять формулу скалярного произведения векторов в координатах; повторили теорию по этой теме; сформировали навык решения задач на нахождение угла между прямыми, между прямой и плоскостью.
Домашняя контрольная работа
Вариант А: № 509 (а);
Вариант Б: № 509 (б), 510 (б);
Вариант В: № 580 (а), 513 (а), 511.
Вариант А
Задача № 509 а). Дано: прямые АВ и CD; А(7; -8; 15), В(8; -7; 13), С(2; -3; 5), D(-1; 0; 4).
Найти: ![]()
Решение: ![]() ,
, ![]()
![]() (Ответ:
(Ответ: ![]() .)
.)
Вариант Б
Задача № 509 б). Дано: прямые АВ и CD; А(8; -2; 3), В(3; -1; 4), С(5; -2; 0), D(7; 0; -2).
Найти: ![]()
Решение: ![]()
![]()
![]() Так как углом между прямыми считают острый угол, то
Так как углом между прямыми считают острый угол, то ![]() (Ответ: 5/9.)
(Ответ: 5/9.)
Задача № 510 б).
Дано: ABCDA1B1C1D1 - куб; М - центр грани BB1С1С (Рис. 6).
Найти: ![]()
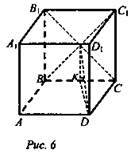
Решение:
1. Рассмотрим ΔDMD1 - равнобедренный; MD = MD1. DD1 = а; Найдем длину MD. Из ΔMKD: ![]() (по теореме Пифагора),
(по теореме Пифагора), ![]() Значит,
Значит, ![]() (теорема Пифагора).
(теорема Пифагора). ![]() Обозначим ∠D1DM = ∠D.
Обозначим ∠D1DM = ∠D.
2. По теореме косинусов ![]()
![]()
![]()
3. ![]() (Ответ: 114°6'.)
(Ответ: 114°6'.)
Вариант В
№ 510 а). Дано: ABCDA1B1C1D1 - куб; М - центр грани ВВ1С1С (см. рис. 1).
Найти: ![]()
Решение:
1. ![]() поэтому
поэтому ![]()
2. Рассмотрим ΔАВМ: ∠В = 90°, АM - наклонная, BM - проекция; ВМ ⊥ В1С (свойство диагоналей квадрата). Тогда по теореме о трех перпендикулярах АМ ⊥ B1C, следовательно, ![]() значит,
значит, ![]() (Ответ:
(Ответ: ![]() )
)
Задача № 513 а). Дано: ABCDA1B1C1D1 - куб; М ∈ ВВ1, ВМ : МВ1 = 3 : 2, N ∈ AD, AN : ND = 2 : 3 (Рис. 7).
Найти: ![]()
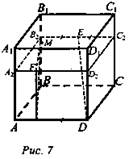
Решение: ММ1 || AD, ND = EM = 3/5a, значит, ЕМ1 = ММ1 — ME = 2/5a. Угол между MN и (DD1C1C), то же самое, что угол между ED и (DD1C1С), а по определению угол между прямой и плоскостью это угол между прямой и ее проекцией на эту плоскость, то есть ![]() DE = МN, а MN найдем из ΔMBN: ∠B = 90°, MB = 3/5а,
DE = МN, а MN найдем из ΔMBN: ∠B = 90°, MB = 3/5а, 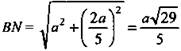 (теореме Пифагора).
(теореме Пифагора). ![]() Отсюда
Отсюда ![]()
![]() (Ответ:
(Ответ: ![]() .)
.)
Задача № 511.
Дано: ABCDA1B1C1D1 - параллелепипед; ∠BAA1 = ∠BAD = ∠DAA1 = 60°; АВ = AA1 = AD = 1 (рис. 8).
Найти: ![]()
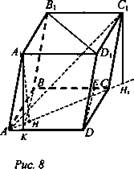
Решение:
1. BB1D1D - прямоугольник, так как BD = DD1 = 1, то BB1D1D - квадрат, значит, ![]() (теореме Пифагора);
(теореме Пифагора); ![]()
2. А1Н ⊥ (ABC) - высота параллелепипеда. А1К ⊥ AD - высота грани (AA1D); так как ∠A = 60°, то АК = 1/2АА1 = 1/2. ВК ⊥ АВ – высота грани (ABC); BK = DE - они разделили АС на 3 равные части ![]() (по т. косинусов) АС2 = 1 + 1 + 1 = 3. Значит,
(по т. косинусов) АС2 = 1 + 1 + 1 = 3. Значит, ![]() Отсюда,
Отсюда, ![]()
![]() (теореме Пифагора).
(теореме Пифагора).
3. Из ΔАС1Н1: ∠H1 = 90°, ![]()
![]()
![]()
![]() Значит,
Значит, ![]() (Ответ:
(Ответ: ![]() )
)