Конус - урок 2 - Конус - ЦИЛИНДР, КОНУС И ШАР

Цели урока:

- закрепление знаний о конической поверхности, конусе;

- умение работать с чертежом и читать его;

- применение знаний в решении задач.

Ход урока

I. Организационный момент

Сообщение темы урока, целей урока.

- Приготовьте необходимые принадлежности: тетрадь, листки с записью фамилии и № варианта, ручку, карандаш, резинку.

- Два ученика идут к доске записывают решение домашнего задания № 548, 549 б). Еще один ученик доказывает формулу площади полной поверхности конуса. Остальные учащиеся отвечают на вопросы математического диктанта.

II. Актуализация опорных знаний

Математический диктант (диктуется по вопросу для каждого варианта). См. приложение.

По окончании диктанта ученики первых парт собирают работы. На обратной стороне доски учащиеся видят ответы. Исходя из настроения детей, возможны объяснения ответов.

I вариант	II вариант
1. Равнобедренный треугольник. 2. Круг. 3. Равнобедренный треугольник. 4. 50 см2. 5.	1. Круг. 2. Прямоугольник. 3. Гипербола. 4. 9 см2. 5.

Проверяем задание домашней работы.

Задача № 548.

Дано: конус, АР = 12 см. ∠PAO = α. a) ∠PAO = 30°. б) ∠PAO = 45°. в) ∠PAO = 60° (рис. 1).

Найти: Sосн.

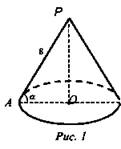
Решение:

1) Из ΔРАО r = ОА = 12 · cos α.

2)

3) Если α = 30°, то если α = 45°, то если α = 60°, то

(Ответ: 108π, 72π, 36π см2..

Задача № 549 б).

Дано: конус, ОР = 8 дм. (рис. 2).

Найти: РO2.

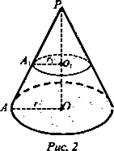
Решение: Сечение и основание конуса - круги - подобные фигуры. ΔАОР ∞ ΔAОР с коэффициентом 1/2. (Ответ: 4 дм.)

III. Решение задач по готовым чертежам

Задачи даются по нарастающей сложности:

1. Дано: Конус, ∠ABC = 120°, АВ = 6 (рис. 3).

Найти: R, Н.

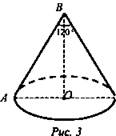
Решение:

1) ΔАВС - равнобедренный, угол при основании ∠A = ∠С = 30°.

2) Из ΔАВО Н = ВО = 3. (Ответ: H = 3, R = 3√3.)

2. Дано: Конус. ΔАВС - равносторонний, АВ = 12, R = 10 (рис. 4).

Найти: OK, Н.

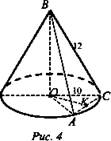
Решение:

1) Из ΔВОС по теореме Пифагора

2) ΔABC - равносторонний, АС = 12, СК = 6. Из ΔСОК по теореме Пифагора ОК2 = ОС2 - СК2, (Ответ: Н = 2√11, ОК = 8.)

IV. Слайд

Высота конуса равна h. Через образующие МА и MB проведена плоскость, составляющая угол α с плоскостью основания. Хорда АВ стягивает дугу с градусной мерой β (рис. 5).

1) Докажите, что сечение конуса плоскостью МАВ - равнобедренный треугольник;

2) Объясните, как построить линейный угол двугранного угла, образованного секущей плоскостью и плоскостью основания;

3) Найдите МС;

4) Составьте (и объясните) план вычисления длины хорды АВ;

5) Составьте план вычисления площади сечения МАВ;

6) Покажите на рисунке, как можно провести перпендикуляр из точки О к плоскости сечения МАВ (обоснуйте построение).

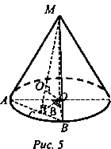
Решение:

1) Образующие конуса равны. Следовательно, стороны ΔМАВ МА = MB, ΔМАВ - равнобедренный.

2) ΔАОВ - равнобедренный, так как две стороны - радиусы окружности. ΔАМВ - равнобедренный, так как две стороны-образующие конуса. Треугольники имеют общее основание. Значит, высоты этих треугольников имеют общую точку - середину основания АВ. По определению линейного угла: угол МСО - является линейным углом двугранного угла, образованного секущей плоскостью МАВ и плоскостью основания конуса.

3) Из ΔСОМ

4) Из ΔСОМ ΔАОВ - равнобедренный. ОС - высота является медианой и биссектрисой. Из ΔВОС - прямоугольный.

5) .

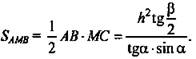6) Плоскость СОМ перпендикулярна плоскости ВАМ, т.к. одна из плоскостей (СОМ) проходит через перпендикуляр к другой (ВС). Поэтому перпендикуляр OO1 к прямой МС является перпендикуляром к плоскости ВАМ.

Учащиеся могут объяснять и по-другому: Строим OO1 ⊥ СМ, получаем OO1 перпендикулярен двум пересекающимся прямым МС и ВС, следовательно, OO1 - перпендикуляр к плоскости ВАМ. В зависимости от уровня класса в 5) и 6) задании можно рассказать только план решения.

V. Решение задач учебника

Задача № 551 а)

Строим чертеж к задаче и обсуждаем:

Назовите длину образующей конуса – 2r.

Какая фигура получается сечением конуса, проходящим через 2 образующие? Равнобедренный треугольник, две стороны которого 2r и угол между ними задан - 30°.

Вспомните и подберите нужную формулу площади треугольника.

Решают самостоятельно. Потом один из учеников проговаривает свое решение. На кодоскопе показать возможную запись.

Дано: конус, MPN - осевое сечение. МР = PN = 2r, ∠APB = 30° (рис. 6).

Найти: S.

Решение: Все образующие конуса 2r, ΔАРВ - равнобедренный, (Ответ: r2.)

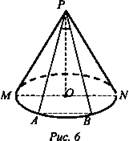
Задача № 553.

Обсуждаем:

Выразите данную формулу Sосев. через высоту и радиус основания: S = RH.

Сколько неизвестных? - 2.

Выразите Sосн. формулой (Sосн. = πr2).

Вывод: Из формулы Sосн., находим r и, подставляя r в формулу Sосн., находим h (рис. 7).

Решение:

1)

2) Из ΔАВР имеем: (Ответ: )

VI. Подведение итогов

Вопросы:

1. Какая фигура получается в сечении конуса плоскостью, проходящей через ось конуса? (Ответ: равнобедренный треугольник.)

2. Какая фигура получается в сечении цилиндра плоскостью, проходящей перпендикулярно оси цилиндра? (Ответ: круг.)

Домашнее задание

П. 55, 56, № 554 а), 555 а), 563.

Решение домашнего задания

Задача № 563. Дано: конус, OP = 1,2 см, Sосев. = 0,6 см2 (рис. 8).

Найти: Sполн.

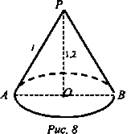
Решение:

1) Осевое сечение - треугольник: высота 1,2 см и основание 2r.

2) Из ΔАОР по теореме Пифагора

3)

(Ответ: 0,9π см2.)

Задача № 554 а).

Дано: конус, l, r, ∠AOB = 60° (рис. 9).

Найти: SABP.

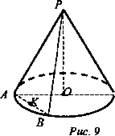
Решение:

1) В ΔАОВ - равносторонний (∠AOB = 60° - угол при вершине равнобедренного ΔАОВ ОА = ОВ = r). Следовательно, АО = ВО = АВ = r.

2) В ΔАРВ стороны АР = ВР = 1, АВ = r; Р = 2l + r; P/2 = l + r. По формуле Герона получим,

(Ответ: )

Задача № 555 а).

Дано: конус, OP = 10 см, ∠PKO = 30°, ∠AOB = 60°.

Найти: SABP.

Решение:

1) ΔKOP - прямоугольный: КР = 2OP; КР = 20 см, так как катет ОР - лежит напротив угла 30° и равен половине гипотенузы КР.

2) ΔАОВ — равносторонний, так как ∠AOB = 60° - при вершине равнобедренного треугольника, ОК - является высотой, биссектрисой. Из ΔBOR ОВ = 20 см. АО = ВО = АВ; АВ = 20.

3)

(Ответ: 200 см2.)