Самостоятельное решение задач - Сфера - ЦИЛИНДР, КОНУС И ШАР

Цель урока:

- закрепить умения по теме: «Цилиндр, конус, сфера, шар».

Ход урока

I. Решение задач

№ 601-628. Ребята решают задачи на местах, затем, желающие выходят к доске и предлагают свое решение. Учитель корректирует ответ.

I уровень

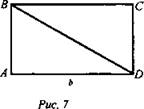
№ 604. При вращении прямоугольника вокруг неравных сторон получаются цилиндры, площади которых равны S1 и S2. Найдите диагональ прямоугольника.

Дано: цилиндры, полученные вращением вокруг стороны АВ и AD; Sп.п. = S1 и Sп.п. = S2 (рис. 7).

Найти: BD.

Решение:

1) При вращении получим цилиндры, у которых радиусы оснований равны АВ = а, AD = b;

2) 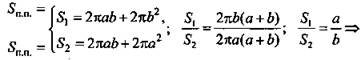подставим в 1-е уравнение системы:

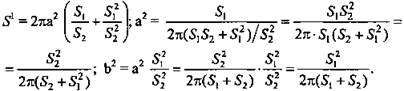
3) Из ΔABD найдем 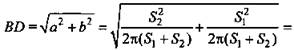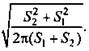(Ответ: )

№ 615. Прямоугольный треугольник с катетами а и b вращается вокруг гипотенузы. Найдите площадь поверхности полученного тела (рис. 2).

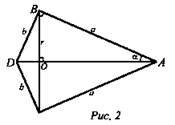
Решение:

1) При вращении треугольника ABD вокруг гипотенузы AD получили два конуса с общим основанием Sбок. = πrl, где r - радиус основания конуса.

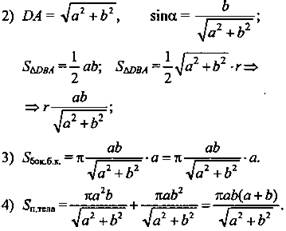
(Ответ: )

№ 618. Диагонали осевого сечения усеченного конуса перпендикулярны. Одно из оснований осевого сечения равно 40 см, а его площадь равна 36 дм2. Вычислите площади боковой и полной поверхности усеченного конуса.

Дано: Усеченный конус, AC, BD - диагонали; AC ⊥ BD. AD = 40 см, SABCD = 36 дм2 (рис. 3).

Найти: Sбок.; Sп.п.

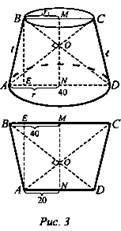
Решение:

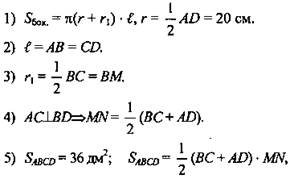но

(Ответ: )

II уровень

1) Докажите, что если одна из граней вписанной в цилиндр треугольной призмы проходит через ось цилиндра, то две другие грани взаимно перпендикулярны.

2) Сфера вписанная в цилиндр (т. е. она касается оснований цилиндра и каждой его образующей). Найдите отношение площади сферы к площади полной поверхности цилиндра.

3) В конусе с углом φ при вершине осевого сечения и радиусом основания r вписана сфера радиуса R (т. е. сфера касается основания конуса и каждой его образующей). Найдите r, если известны R и φ.

№ 1. Решение:

Дано: цилиндр, АВСА1В1С1 - треугольная призма, AA1B1B проходит через OO1 (рис. 4).

Доказать: AA1C1C ⊥ BCC1B1.

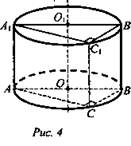
Доказательство:

1) АВ - диаметр основания цилиндра ∠ACB = 90°, BС ⊥ СС, CC1 перпендикулярна основанию цилиндра;

2) Так как СС( перпендикулярна основанию, то ВС ⊥ АСС1, значит, угол между плоскостями равен 90°, по признаку перпендикулярности 2-х плоскостей ⇒ АА1С1С ⊥ BСС1В1, что и требовалось доказать.

№ 2. Решение:

1) В цилиндр можно вписать сферу, если его осевое сечение квадрат (рис. 5).

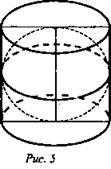
2) Пусть R - радиус цилиндра, тогда R радиус сферы, a h = 2R.

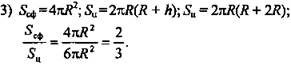
(Ответ: 2/3.)

№ 3. Дано: Конус, в который вписана сфера радиуса R, ∠ACB = φ (рис. 6).

Найти: rк.

Решение:

1) В любой конус можно вписать сферу.

2) O1В = r, a OL = R, ∠FCD = φ.

3) Из ΔACB: ∠ABC = 90° - φ/2.

4) ВО - биссектриса ∠B, ∠O1BO = 45° - φ/2.

5)

(Ответ: )

III уровень

Осевое сечение конуса есть треугольник с углом 120°. Радиус основания конуса - 6 м. Найдите площадь сечения, проходящего через две образующие, угол между которыми 30° (рис. 7).

Дано: R = 6 м, ∠ASB = 120°.

Найти: Sceч.

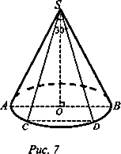
Решение:

1)

2) Из ΔOSВ находим SB.

3)

4) Из ΔSOB:

5)

(Ответ: 12 см2.)

II. Подведение итогов

Домашнее задание

Разгадать кроссворд на тему «Тела и фигуры вращения»

По горизонтали: 1. Фигура на плоскости, все точки которой расположены не далее данного расстояния от одной точки. 2. Прямая, при вращении которой вокруг оси образуется боковая поверхность цилиндра, конуса. 3. Тело, полученное вращением прямоугольника вокруг одной из его сторон. 4. Угол между высотой и плоскостью основания конуса. 5. Тело, полученное вращением круга вокруг оси, лежащей в плоскости круга и не пересекающей его.

По вертикали: 1. Тело, полученное вращением прямоугольного треугольника вокруг одного из его катетов. 2. Плоская фигура, при вращении которой образуется усеченный конус. 3. Тело вращения, являющееся верхней частью архитектурного сооружения. 4. Отрезок, соединяющий две точки сферы и проходящий через центр шара. 5. Тело, полученное вращением полукруга вокруг его диаметра, б. Фигура, полученная вращением полуокружности вокруг ее диаметра. 7. Тело вращения, об устойчивости движения которого написана известная работа великой русской женщины-математика.

Ответы:

По горизонтали: 1. Круг. 2. Образующая. 3. Цилиндр. 4. Прямой. 5. Тор.

По вертикали: 1. Конус. 2. Трапеция. 3. Купол. 4. Диаметр. 5. Шар. 6. Сфера. 7. Юла.