Поурочные разработки по Геометрии 11 класс
Объем шара - Объем шара и площадь сферы - ОБЪЕМЫ ТЕЛ
Цель урока:
- вывести формулу объема шара, показать ее применение при решении задач.
Ход урока
I. Организационный момент
Сообщить тему урока, сформулировать цели урока.
II. Актуализация опорных знаний
Теоретический опрос (фронтальная работа с классом).
- Дайте определение, что называется шаром, радиусом и диаметром шара?
- Дайте определение площади поверхности шара. Запишите формулу площади поверхности шара (S = 4πR2).
III. Изучение нового материала
- Мы уже рассмотрели формулы для вычисления объемов некоторых многогранников и круглых тел. (На доске иллюстрации с изображением многогранников и круглых тел).
- Давайте вспомним и запишем под каждой фигурой уже известные нам формулы объемов.
![]()
![]()
Задумывались ли вы над таким вопросом: как давно появились эти формулы, и кто первым открыл их?
Еще до нашей эры формулы объемов многих тел (параллелепипеда, призмы и цилиндра) были известны.
Позднее, благодаря трудам древнегреческих ученых Демокрита, Евклида и Архимеда были открыты формулы для вычисления объемов пирамиды, конуса, шара и других тел.
В современных учебниках формулы для вычисления объемов пирамиды, конуса и шара выводятся на основе интегральной формулы. Но этот простой и изящный способ появился благодаря трудам И. Ноготыса и Г. Лейбница гораздо позднее того как были открыты сами формулы. Изучим и мы доказательство формулы ![]() (Показать портреты ученых, о которых было упомянуто в разговоре.)
(Показать портреты ученых, о которых было упомянуто в разговоре.)
Для доказательства используем метод координат, который ввел в геометрию Р. Декарт.
Рассмотрим шар радиуса Я с центром в точке О и выберем ось ох произвольным образом. Сечение шара плоскостью, перпендикулярной ох, является кругом с центром в т. М ∉ ох и радиусом R.
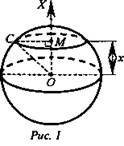
Обозначим площадь сечения S(x), где х - абсцисса точки М.
Из ΔОМС ![]() Тогда
Тогда ![]() где –R ≤ х ≤ R.
где –R ≤ х ≤ R. 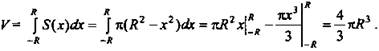
Теорема об объеме шара доказана.
В практических приложениях часто указывается диаметр шара, поэтому в процессе решения задач полезно использовать формулу: ![]() где D - диаметр шара.
где D - диаметр шара.
IV. Формирование умений и навыков учащихся
1. Работа в рабочих тетрадях:
а) разобрать и записать решение задачи № 710 в) (краткое решение).
Дано: шар, S = 64π см2.
Найти: R и V.
Решение: Так как ![]() имеем
имеем ![]() Тогда
Тогда ![]() (Ответ: R = 4 см,
(Ответ: R = 4 см, ![]() )
)
б) задача № 712.
Дано: Vшара = Vцил., Dшара = Dцил.
Выразить Hцил. через R.
Решение. ![]() (Ответ: Н = 4/3R.)
(Ответ: Н = 4/3R.)
в) разобрать и записать в тетрадях вопрос № 9 к главе VII (стр. 161).
(Ответ: ![]() )
)
Дополнительная задача.
На надгробном камне могилы Архимеда в Сиракузах изображен цилиндр с вписанным в него шаром. Это символ открытия формул объема шара и площади сферы, а также важного вывода, что «объем шара, вписанного в цилиндр, в ... раз меньше объема цилиндра и что также относятся поверхности этих тел». Найдите отношение объема шара к объему цилиндра и отношение площади шара к площади поверхности цилиндра.
Решение: Вспомнив формулы, о которых говорилось в условии задачи, запишем отношение 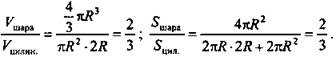
Эти отношения и соотношения следует выделить и запомнить.
V. Подведение итогов
- Чему равно отношение объема шара к объему цилиндра, если их радиусы равны?
Домашнее задание
П. 71 № 710 а), б); 711, 713 (выучить доказательство теоремы). Дополнительная задача: Из деревянного равностороннего цилиндра выточен наибольший возможный шар. Сколько процентов материала сточено? Решение:
1) Из условия задачи вытекает, что высота цилиндра H = 2R, подставим значение Н в формулу объема цилиндра: ![]()
2) Объем шара ![]()
3) Найдем, сколько сточено материала: ![]()
4) Найдем, сколько % составляет сточенный материал: 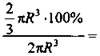
![]() (Ответ:
(Ответ: ![]() )
)