Повторение. Цилиндр, конус и шар, площади их поверхностей - ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 10-11 КЛАССОВ

Цели урока:

- систематизировать теоретические знания по темам;

- совершенствовать навыки решения задач.

Ход урока

I. Организационный момент

II. Актуализация знаний учащихся

Повторение теории по таблицам. Учащиеся в течение 5-7 минут самостоятельно повторяют теорию используя таблицы.

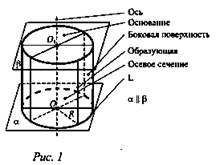
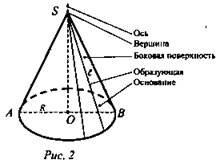
А. Цилиндр (рис. 1) OO1 = Н- высота цилиндра.	Б. Конус (рис. 2) SO = H - высота; l - образующая;
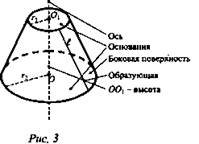
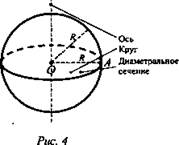
В. Усеченный конус (рис. 3)	Г. Шар (рис. 4)

III. Решение задач по готовым чертежам.

1. (рис. 5).

Найти: S6ок.

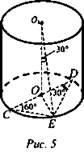
Решение:

1) ΔСОЕ - равнобедренный треугольник, так как СО = ОЕ ⇒ ∠OEC = 60°.

2) ∠CED - вписанный, ∠CED = 90°, ∠CDE = 30°.

3) .

4) R = 10√3.

5) ΔОО1E - прямоугольный, ∠OO1E = 30°. OO1 = H = 30.

6) (Ответ: )

2. (рис. 6).

SCC1D1D = Q, Sбоков. — ?

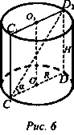
Решение:

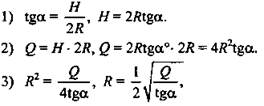
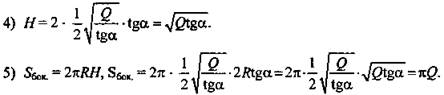(Ответ: πQ.)

3. (рис. 7).

SO = 15. A1B1, W(O1; O1A1) - сечение конуса.

Sполн. - ?

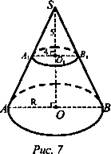
1) ΔA1O1S ~ ΔAOS по 2-м углам, значит,

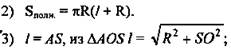
4) (Ответ: )

4. (рис. 8)

ΔABC - правильный, OO1 = 3.

Sш. - .

Sсеч.CAB — ?

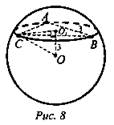
1) ΔCO1O - прямоугольный, СО = Rш.

2) O1С = r, r - радиус описанной окружности около

3)

4) ΔСО1О - прямоугольный

5) (Ответ: 48π.)

IV. Решение задач

1. Прямоугольная трапеция с основаниями 6 см и 10 см и высотой 3 см вращается около большего основания. Найдите площадь поверхности тела вращения. (Ответ: 60 см2.)

2. Прямоугольная трапеция с основаниями 12 см и 20 см и высотой 15 см в первый раз вращается около меньшего основания, а во второй - около большего. Сравните площади поверхностей тел вращения. (Ответ: в первом случае на 240π см2 больше.)

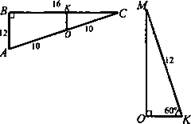
3. В конус вписана пирамида МАВС, основанием которой служит прямоугольный треугольник с катетами АВ = 12 см и ВС = 16 см. Двугранный угол при катете ВС равен 60°. Найдите: а) площадь грани MВС; б) площадь боковой поверхности конуса.

4. Высота конуса равна h, образующая равна l. Найдите радиус описанного около конуса шара.

Решение:

1. (рис. 9).

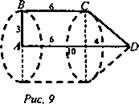
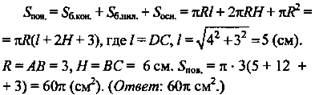
2. (рис. 10)

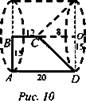
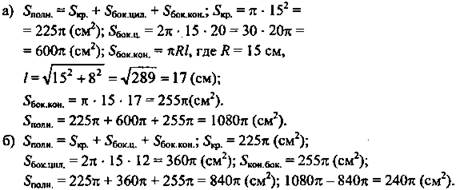
(Ответ: на 240π см2 в первом случае больше.)

3. (рис. 11)

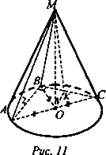
a) 1) ∠OKM = 60° - линейный угол двугранного угла ОВСМ (ОК ⊥ ВС, МК ⊥ ВС);

2) (так как ΔАВС - прямоугольный).

3) Так как ΔABC - прямоугольный, то О - середина гипотенузы и центр описанной окружности.

4) ОК - средняя линия ΔABC (ОК ⊥ АВ, АВ ⊥ ВС ⇒ ОК || АВ; О - середина А С ⇒ К - середина ВС).

5) ΔОМК – прямоугольный (ОМ ⊥ ABC), ∠ОМК = 30° ⇒ МК = 12 см.

6)

б) 1) Из ΔОМК:

2) ΔВОМ - прямоугольный: BM = l.

3) (Ответ: )

4. (рис. 12).

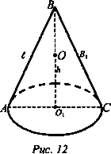
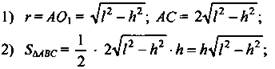
3) - радиус описанной окружности около ΔАВС со сторонами а, b, с, площадью S. 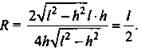(Ответ: 1/2.)

V. Подведение итогов

- Назовите основные элементы а) цилиндра; б) конуса.

Домашнее задание

1) Повторить главу VI, § 1, 2, 3.

2) Решить оставшиеся нерешенными на уроке задачи.