Поурочные разработки по Геометрии 11 класс
Простейшие задачи в координатах - урок 2 - Координаты точки и координаты вектора - МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
Цели урока:
- показать примеры решения стереометрических задач координатно-векторным методом;
- совершенствовать навыки решения задач.
Ход урока
I. Организационный момент
Сообщить тему урока, сформулировать цели урока.
II. Актуализация опорных знаний
1. Теоретический опрос:
а) Вывести формулу координат середины отрезка.
б) Вывести формулу длины отрезка.
2. Проверка домашнего задания:
Один ученик на доске записывает решение домашнего задания № 429.
Дано: М(-4; 7; 0) N(0; -1; 2).
Найти: расстояние от начала координат до середины отрезка MN.
Решение: Пусть К - середина отрезка MN, тогда ![]() Значит,
Значит, ![]()
3. Индивидуальная дифференцированная работа на карточках (см. приложение).
4. Математический диктант (см. приложение).
Решение индивидуально-дифференцированных задани.
Карточка № 1
1) Дано: ![]()
Найти: координаты ![]()
Решение: ![]()
![]() (Ответ:
(Ответ: ![]() .)
.)
2) Дано: ![]() коллинеарные.
коллинеарные.
Найти: m и n.
Решение: По определению коллинеарных векторов ![]() k = -3. Значит, n = -3 · 1; n = -3, 3 = -3 · m; m = -1. Так как k < 0, то
k = -3. Значит, n = -3 · 1; n = -3, 3 = -3 · m; m = -1. Так как k < 0, то ![]() ;
; ![]() Видно
Видно ![]() (Ответ: n = -3; m = -1;
(Ответ: n = -3; m = -1; ![]() .)
.)
Карточка № 2
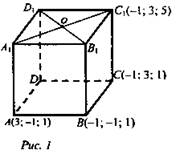
1) Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед (рис. 1).
а) Найти: координаты точек B1; D1.
б) Разложить ![]() по координатам векторов
по координатам векторов ![]()
Решение:
а) Так как параллелепипед прямоугольный, то координаты В1(-1; -1; 5); А1(3; -1; 5). Используя формулу координат середины отрезка, ![]() O(1; 1; 5). Найдем координаты D1:
O(1; 1; 5). Найдем координаты D1: 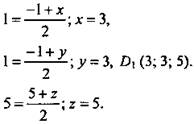
б) ![]()
![]()
(Ответ: а) В1(-1; -1; 5); D1(3; 3; 5), б) ![]() .)
.)
2) Дано: А(6; -1; 0), В(0; 3; -2), С(3; 1; -1).
Доказать: точки А, В, С лежат на одной прямой.
Решение: Если векторы ![]() коллинеарные, то точки А, В, С лежат на одной прямой, в противном случае - не лежат на одной прямой. Найдем координаты векторов
коллинеарные, то точки А, В, С лежат на одной прямой, в противном случае - не лежат на одной прямой. Найдем координаты векторов ![]() ;
; ![]()
![]() Очевидно,
Очевидно, ![]() значит, векторы
значит, векторы ![]() коллинеарные, и, следовательно, точки А, В, С лежат на одной прямой.
коллинеарные, и, следовательно, точки А, В, С лежат на одной прямой.
Карточка № 3
1) Дано: А(2; -1; 0), В(-3; 2; 1), С(1; 1; 4); ![]()
Найти: координаты точки D.
Решение: Найдем координаты векторов ![]() если D(х; у; z),
если D(х; у; z), ![]() Пользуясь условием
Пользуясь условием ![]() составим уравнения для координат векторов
составим уравнения для координат векторов ![]() и
и ![]() .
. 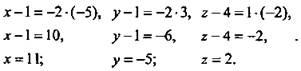 (Ответ: D(11; -5; 2).)
(Ответ: D(11; -5; 2).)
2) Дано: А(1; 1; 1), В(-1; 0; -1), С(0; 2; 2), D(2; 0; 0). Лежат ли эти точки в одной плоскости?
Решение: Найдем координаты векторов ![]()
![]() Пусть
Пусть ![]()
![]() Пусть
Пусть ![]()
![]() Пусть
Пусть ![]() Условие компланарности векторов:
Условие компланарности векторов:
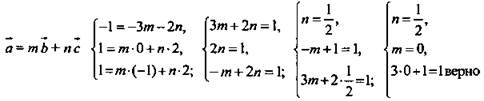
Итак, признак компланарности выполняется, значит, по определению векторы ![]() компланарны и, следовательно, точки А, В, С, D лежат в одной плоскости. (Ответ: точки лежат в одной плоскости.)
компланарны и, следовательно, точки А, В, С, D лежат в одной плоскости. (Ответ: точки лежат в одной плоскости.)
Проверяются ответы диктанта, домашнего задания, вывод формул, собираются работы по индивидуальным карточкам.
III. Формирование умений и навыков учащихся
Фронтальная работа с классом.
Задача № 425 г)
Дано: А (7; 2m+n; -n); В(-5; -3; m-3); К - середина отрезка АВ; k ∈ Ох.
Найти: m; n.
Решение: Так как k ∈ Ох, то k(х; 0; 0). Используя формулы координат середины отрезка АВ, имеем
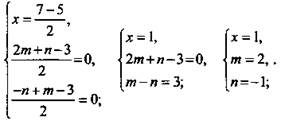 (Ответ: m = 2; n = -1..
(Ответ: m = 2; n = -1..
Задача № 427.
Дано: ![]()
Найти: ![]()
Решение: ![]()
![]() (Ответ:
(Ответ: ![]() .)
.)
Какие виды треугольников по сравнению длин сторон вы можете назвать.
Как определить вид треугольника в зависимости от длин сторон?
Задача № 431 б).
Дано: ΔАВС; А(3; 7; -А), В(5; -3; 2), С(1; 3; -10).
Определить вид ΔABC.
Решение: ![]()
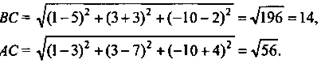
Проверим равенство BС3 = AC2 + AB2; 196 = 140 + 56 верно ⇒ по теореме обратной теоремы Пифагора сделаем вывод, что ΔABC прямоугольный с прямым углом А.
Решение задач повышенного уровня сложности
a) Дано: А(2; 5; 8), В(6; 1;0).
На оси ординат найти точку С, равноудаленную от точек А и В.
Найти: площадь ΔABC.
Решение:
1) По условию С ∈ оси OY ⇒ С(о; у; о) и АС = ВС, тогда АС2 = ВС2. По формуле расстояния между точками составим уравнение относительно у: (0 - 2)2 + (у - 5)2 + (0 - 8)2 = (0 - 6)2 + (у - 1)2 + (0 - 0)2, 4 + (у - 5)2 + 64 = 36 + (у - 1)2, (у - 5)2 - (у - 1)2 + 32 = 0, у2 – 10y + 25 – y2 + 2у - 1 + 32 = 0, -8y = -56, у = 7, С(0; 7; 0).
2) ΔАВС - равнобедренный ⇒ D - середина АВ (рис. 2);
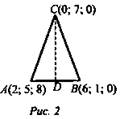
![]()
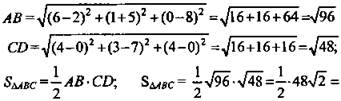
![]() (Ответ: С(0; 7; 0); SΔABC =
(Ответ: С(0; 7; 0); SΔABC = ![]() )
)
б) Дано: ![]() коллинеарные,
коллинеарные, ![]()
Найти: координаты ![]()
Решение: Так как ![]() коллинеарные по условию, то
коллинеарные по условию, то ![]() По правилу вычитания векторов:
По правилу вычитания векторов: ![]()
![]() По условию
По условию ![]()
![]()
![]() (Ответ:
(Ответ: ![]() или
или ![]() )
)
IV. Подведение итогов
- Сегодня на уроке мы продолжали отрабатывать умение и навыки решения стереометрических задач координатно-векторным методом. Применяли данный метод для решения задач повышенного уровня сложности.
Домашнее задание
I уровень: задачи № 430; 431 а), в), г); 432.
Решение задач I уровня.
Задача № 430.
Дано: А(3/2; 1; -2), В(2; 2; -3), С(2; 0; -1) (рис. 1).
Найти: а) РΔABC б) медианы ΔABC.
Решение:
а) По формуле расстояния между двумя точками найдем длины сторон ΔАВС:
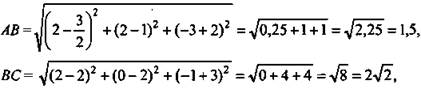
![]()
Итак, ΔABC - равнобедренный, АВ = АС. ![]()
б)Так как ΔABC равнобедренный, то медианы ВК и CN равны, где точки M, N, К - середины сторон. ![]()
![]()
![]()
![]() (Ответ:
(Ответ: ![]() ).
).
Задачи № 431 а), в), г).
а) Дано: ΔАВС; А(9; 3; -5), В(2; 10; -5), С(2; 3; 2).
Определить: вид ΔABC.
Решение:
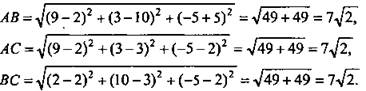
АВ = АС = ВС ⇒ ΔАВС - равносторонний.
б) Дано: ΔABС; A(5; -5; -1), В(5; -3; -1), С(4; -3; 0).
Определить: вид ΔABC.
Решение: ![]()
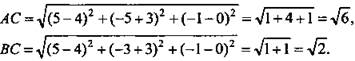
Проверим равенство ![]() 6 = 6. Следовательно, по теореме обратной теореме Пифагора делаем вывод, что ΔАВС - прямоугольный с гипотенузой AС.
6 = 6. Следовательно, по теореме обратной теореме Пифагора делаем вывод, что ΔАВС - прямоугольный с гипотенузой AС.
в) Дано: ΔАВС; А(-5; 2; 0), В(-4; 3; 0), С(-5; 2; -2).
Определить: вид ΔАВС.
Решение: ![]()
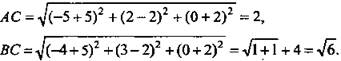 Проверим равенство
Проверим равенство ![]() 6 = 2 + 4, 6 = 6 верно. Значит, ΔABC - прямоугольный с гипотенузой ВС.
6 = 2 + 4, 6 = 6 верно. Значит, ΔABC - прямоугольный с гипотенузой ВС.
Задача № 432.
Дано: А(-3; 4; -4).
Найти: а) расстояние от А до координатных плоскостей; б) расстояние от А до осей координат.
Решение:
а) Точка А1 - проекция точки А на плоскость хОу имеет координаты A1(-3; 4; 0), поэтому расстояние от А до хОу равно АА1; ![]() Точка А2 - проекция точки А на плоскость yOz имеет координаты А2(0; 4; -4), поэтому расстояние от А до yOz равно АА2;
Точка А2 - проекция точки А на плоскость yOz имеет координаты А2(0; 4; -4), поэтому расстояние от А до yOz равно АА2; ![]() Точка А3 - проекция точки А на плоскость хOz имеет координаты А3(-3; 0; -4), поэтому расстояние от А до xOz равно АА3;
Точка А3 - проекция точки А на плоскость хOz имеет координаты А3(-3; 0; -4), поэтому расстояние от А до xOz равно АА3; ![]()
б) Проекция точки А на ось Ох точка Ах(-3; 0; 0), поэтому ![]() Проекция точки А на ось Оу точка Ау(0; 4; 0), поэтому
Проекция точки А на ось Оу точка Ау(0; 4; 0), поэтому ![]() Проекция точки А на ось Oz точка Az(0; 0; -4), поэтому расстояние
Проекция точки А на ось Oz точка Az(0; 0; -4), поэтому расстояние ![]()
II уровень: задачи № 437; 435 (рассмотреть 2 случая) и задача:
Дано: ![]() вектора
вектора ![]() коллинеарные.
коллинеарные.
Найти: m; n.
Решение задач II уровня.
Задача № 437.
Дано: А(-2-, 3; 5), В(3; 2; -3).
Найти: точку, равноудаленную от А и В на оси: а) Ох; б) Оу; в) Oz.
Решение:
а) Пусть точка М(х; 0; 0) искомая. По условию АМ = ВМ. Составим уравнение: ![]()
![]() .
.
б) Пусть точка N(0; y; 0) искомая. Решим уравнение: AN = BN; ![]()
![]()
в) Пусть точка К(0; 0; z) искомая. Решим уравнение: АК = ВК; АК2 = ВК2, ![]()
![]()
(Ответ: (-1,6; 0; 0), (0; 8; 0), (0; 0; 1).)
Задача № 435.
Дано: А(1; 0; k), В(-1; 2; 3), С(0; 0; 1).
При каких значениях к ΔАВС - равнобедренный?
Решение:
1. Пусть АВ = АС, тогда АВ2 = АС2. Составим и решим уравнение: ![]()
![]()
2. Пусть АВ = ВС, тогда АВ2 = ВС2. ![]() 3 - k = 1 или 3 - k = -1, k = 2 или k = 4.
3 - k = 1 или 3 - k = -1, k = 2 или k = 4.
3. Пусть АС = ВС, тогда AC2 = BC2. ![]()
![]() или
или ![]() или
или ![]()
(Ответ: ![]() .)
.)
Дополнительная задача.
Дано: ![]() вектора
вектора ![]() - коллинеарные.
- коллинеарные.
Найти: m; n.
Решение: По условию вектор ![]() имеет координаты
имеет координаты ![]() вектор
вектор ![]() имеет координаты
имеет координаты ![]() Известно, что векторы
Известно, что векторы ![]() и
и ![]() коллинеарные, ⇒ выполняется условие:
коллинеарные, ⇒ выполняется условие: ![]() Исходя из этого условия, составим и решим систему:
Исходя из этого условия, составим и решим систему: ![]() (Ответ: m = 2; n = 6.)
(Ответ: m = 2; n = 6.)