Угол между векторами. Скалярное произведение векторов - Скалярное произведение векторов - МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ

Цели урока:

- ввести понятие угла между векторами и скалярного произведения векторов, рассмотреть формулу скалярного произведения в координатах;

- показать применение скалярного произведения векторов при решение задач.

Ход урока

I. Организационный момент

II. Актуализация знаний учащихся

1. Анализ контрольной работы.

Подводятся итоги контрольной работы и разбираются типичные ошибки.

2. Проверка домашнего задания.

Задача № 439 а) (на доске записать заранее и проверить с учащимися).

Дано: О(0; 0; 0), А(4; 0; 0), В(0; 6; 0), ΔAОВ - прямоугольный (рис. 1).

Найти: 1) К(х; у; z) - центр окружности, описанной около ΔAОВ; 2) АК = R.

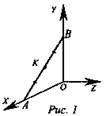
Решение: Центр окружности К - середина гипотенузы АВ. Найдем координаты точки К; (Ответ: (2; 3; 0); √13.)

3. Устные упражнения

Решение задач с целью подготовить учащихся к восприятию нового материала. Фронтальная работа с классом: отвечает один из учащихся, остальные при необходимости дополняют, исправляют ответ своего товарища.

Векторы в пространстве (рис. 2).

1. Дано: А(-3; -2; 4), В(-4; 3; 2).

Найти:

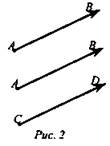
2. Дано: А(2; -3; 1), В(4; -5; 0), С(5; 0; -4), D(7; -2;-3).

Равны ли векторы ?

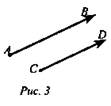
3. Коллинеарные ли векторы , если А(1; -3; 4), В(5; 1; -2), С(2; 0; 1), D(4; -2; 2) (рис. 3).

III. Изучение нового материала

Рис. 126 (учебника)

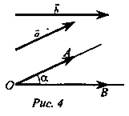
1. Ввести понятие угла между векторами (рис. 4). Если то если то если то

Рис. 127 (учебник)

2. Ввести понятие скалярного произведения векторов.

Скалярное произведение двух векторов есть произведение их длин на косинус угла между ними.

Обозначение: Отсюда 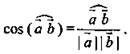Обратить внимание, что - число (скаляр). Скаляр - лат. scale - лестница, шкала. Ввел в 1845 г. У. Гамильтон, английский математик.

3. Пример применения скалярного произведения в физике (рис. 5).

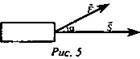
Пусть под действием постоянной силы тело совершило механическое перемещение, которое задается вектором Если то для вычисления работы А, совершенной силой , используют формулу что по определению является скалярным произведением

4. Доказательство утверждений рассматриваются по усмотрению учителя (в учебнике они предполагаются для самостоятельной работы).

Утверждение 1. Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

Доказательство:

1) Пусть тогда значит,

2) Пусть тогда Но (ненулевые), значит,

Утверждение 2. Скалярный квадрат вектора равен квадрату его длины.

Доказательство: Угол между равными векторами 0°, cos0° = 1.

Имеем

5. Формула скалярного произведения двух векторов и

Через их координаты

Скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.

Приведем доказательство формулы скалярного произведения в координатах для случая, когда векторы неколлинеарные (рис. 6).

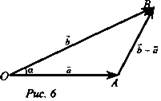
По теореме косинусов

Так как то это равенство можно переписать в таком виде или откуда Пусть тогда вектор имеет координаты Подставив эти выражения в равенство (1),

IV. Закрепление изученного материала. Формирование умений и навыков учащихся

1. Устно.

Дан куб ABCDA1B1C1D1 (рис. 7).

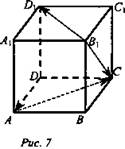
Найдите угол между векторами

a)

б)

в)

(Ответы: а) 45°; б) 45°; в) 135°.)

2. Решение задач № 443 (а, г).

Дано: ABCDA1B1C1D1 - куб, АВ = а, O1 - центр грани A1B1C1D1.

Найти:

Решение: а) Так как то

Способ 1.

Треугольник ВА1С1 правильный. Стороны его равны как диагонали равных квадратов: поэтому

Способ 2.

Способ 3.

Введем прямоугольную систему координат (рис. 8).

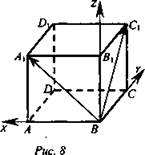
Вектор имеет координаты {а; 0; а}, а вектор имеет координаты {0; а; а). Поэтому

Дополнительная задач.

Вычислите угол между вектором и координатным вектором

Решение:

(Ответ: 48°11’.)

3. Решить самостоятельно (по группам).

1 группа № 443 д); 2 группа № 443 е); 3 группа № 443 ж).

Ответы:

V. Подведение итогов

- Сегодня на урюке мы рассмотрели понятия угла между векторами скалярного произведения векторов. Вывели формулу для вычисления скалярного произведения в координатах, а также усвоили, что скалярное произведение перпендикулярных векторов равно «0» и, если скалярное произведение векторов равно «0», то векторы перпендикулярны.

Домашнее задание

П. 46; 47 (до свойств). I уровень № 441 в-з). II уровень № 443 б), в). III уровень.

Задача. Все ребра тетраэдра ABCD равны друг другу. Точки М и N— середины ребер AD и ВС (рис. 9).

Докажите, что

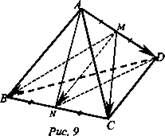
Решение:

Способ 1.

ВМ - медиана, а значит, и высота в правильном треугольнике ABD. Поэтому Аналогично Следовательно,

Способ 2.

AN = DN как высоты равных правильных треугольников, поэтому треугольник AND равнобедренный. Следовательно, медиана NM является также высотой треугольника AND, то есть